공데셍

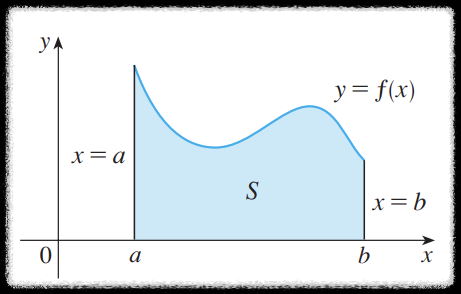
일변수 함수에서 적분은 정의역이 직선형태였고 이 직선을 따라서 적분을 했었다. 평면 위의 곡선으로 정의된 정의역에 대해서도 구불구불하게 적분을 할 수 있지 않을까 생각해보자. 무슨 말이냐면, 일반적인 적분은 다음 그림과 같은데 정의역이 평면 위의 곡선이라면 다음 그림과 같이 적분할 수도 있지 않을까 생각해볼 수 있다는 말이다. 이러한 적분을 선적분(Line Integral) 이라고 부르는데, (왜 곡선적분이 아니라 선적분인지는 알 수 없다.) 선적분을 정의하기 위해 다음과 같이 정의된 곡선 $C$ 를 고려하자. $$ C \; : \; x = x(t), \; y = y(t), \quad a \le t \le b $$ 이는 다음과 같은 벡터 함수로 생각할 수 있다. $$ \textbf{r}(t) = $$ 이..

새로운 단원을 본격적으로 들어가기에 앞서 벡터장과 스칼라장에 대해 새롭게 알 필요가 있다. 벡터장은 어떠한 평면 또는 공간의 좌표마다 벡터를 대응시킨 것이고 스칼라장은 어떠한 평면 또는 공간의 좌표마다 스칼라 값을 대응시킨 것이다. 즉, 좌표를 정의역으로 갖고 벡터 또는 스칼라를 공역으로 갖는 함수인 것이다. 벡터장의 예로는 어떤 방 안에 공기의 흐름이 존재한다고 하자. 이 때 방 안의 모든 위치마다 바람의 방향, 세기가 존재할 것인데, 이를 각 좌표마다 대응되는 방향과 세기를 표시해준 것이 벡터장이다. (벡터장은 앞서 배웠던 벡터함수 $\textbf{r}(t) = $ 랑 실질적으로는 같은 것이다. $t$ 변수를 생각하지 않고 $x,y,z$ 에 대한 함수라고 보면, $\textbf{r}(t)$ 는 $\t..

본 블로그의 미적분학 17번~24번 포스팅에 관한 연습문제이다. 17. 넓이 문제와 정적분 18. 정적분의 성질 19. 미적분학의 기본정리 20. 부정적분 21. 치환 적분 22. 부분 적분 23. 적분을 이용한 부피 계산 24. 함수의 평균값 1. 다음을 증명하여라 $$ \int_{0}^{\frac{\pi}{2}} x \sin{x} \; dx \le \dfrac{\pi^2}{8} $$ 더보기 $\sin{x} \le 1$ 이므로 $[0, \dfrac{\pi}{2}]$ 에서 $x\sin{x} \le x$ 이다. 따라서 정적분의 비교 성질에 의하면 $$ \textcolor{orange}{\int_0^{\frac{\pi}{2}} x \sin{x} \; dx} \textcolor{blue}{\le} \int_0..

$n$ 개의 값 $y_1, y_2, y_3, \cdots , y_n$ 의 평균은 다음과 같이 정의된다. $$ y_{\text{avg}} = \dfrac{y_1 + y_2 + y_3 + \cdots + y_n}{n} = \dfrac{1}{n}\sum_{i = 1}^n y_i $$ 무한히 많은 값을 갖는 함수에 대해서도 평균을 생각할 수 있다. 예를 들어 연속함수 $f(x) = x^2$ 의 $[0, 2]$ 에서의 평균은 다음과 같이 생각할 수 있다. $x = 0$ 일 때 $y = f(0) = 0$ $x = 0.000...1$ 일 때 $y = f(0.000...1) = (0.000...1)^2$ $x = 0.000...2$ 일 때 $y = f(0.000...2) = (0.000...2)^2$ ... $x = ..

넓이 계산하는 파트는 책만 읽어도 쉽게 이해 되므로 생략했다. 다음과 같은 물체를 살펴보자. 물체는 $x = a$ 부터 $x = b$ 까지의 범위에 분포해 있다. 임의의 점 $x$ 에서의 단면의 넓이를 $A(x)$ 라고 하자. 이 물체의 부피를 다음과 같이 $x$ 축에 평행하게 여러번 잘라 낸 부분 부피들의 합으로 근사시킬 수 있다. 예컨대, 7개 조각으로 나눈 위의 경우엔 부피 $V$ 는 다음과 같이 근사된다. $$ V \approx \sum_{i = 1}^7 A(x_i) \cdot \Delta x$$ 정적분에서 넓이를 구할 때처럼, 나눈 조각의 갯수가 많아질수록 실제 부피에 수렴하게 될 것으로 예상할 수 있다. 따라서 부피를 다음과 같이 정의한다. 부피의 정의 (정적분) $S$ 가 $x = a$ 와 ..

이번에는 적분을 할 때 이용되는 또 다른 테크닉인 부분 적분을 소개한다. $x$ 에 대한 함수 $f$ 와 $g$ 에 대해 미분 공식 중 곱의 공식은 다음과 같다. $$ \dfrac{d}{dx}[fg] = f'g + fg' $$ 이 식의 양변을 부정적분해주면 다음과 같다. $$ \begin{align} fg = &\int f'g + fg' \; dx \\ = &\int f'g \; dx + \int fg' \; dx \end{align} $$ 식을 재정렬하면 $$ \int f'g \; dx = fg - \int fg' \; dx$$ 여기서 $f$ 는 적분될 함수이고 $g$ 는 미분될 함수이다. 우리는 $f$ 가 적분되거나 $g$ 가 미분되면서 식이 더 간단해지길 바란다. 다음 예제를 통해 무슨 말인지 설명..

앞서 잘 알려진 함수들에 대한 부정적분 공식을 살펴보았다. 하지만 대부분의 경우에는 역도함수가 무엇인지 찾기 쉽지 않다. 예를 들어 다음 식의 역도함수는 무엇인지 바로 떠오르지 않을 것이다. $$ \int 2x\sqrt{1 + x^2} dx $$ 하지만 $1 + x^2 = u$ 라고 치환하면 $2x dx = du$ 이므로 다음과 같다. $$ \int 2x\sqrt{1 + x^2} dx = \int \sqrt{u} du = \int u^{\frac{1}{2}} du = \dfrac{2}{3}u^{\frac{3}{2}} + C $$ 이제 $u = 1 + x^2$ 를 대입해주어 부정적분을 마무리할 수 있다. $$ \int 2x\sqrt{1 + x^2} dx = \dfrac{2}{3}(1 + x^2)^{\fra..

미적분학의 기본정리를 통해 적분이 미분의 역연산임을 알 수 있었다. 이제는 역도함수를 적분의 기호를 통해 표현할 수 있다. 앞으로는 $f$ 의 역도함수 $F$ 를 다음과 같은 기호로 표현하기로 한다. $$ \int f(\textcolor{red}{x}) d\textcolor{red}{x} = F(\textcolor{red}{x}) $$ 예를 들면 $\int x^2 dx = \dfrac{x^3}{3} + C$ 이다. 정적분의 결과는 값이였던것과 달리 부정적분의 결과는 함수임을 인지하자. (정확히는 Family of function 이다.) 다음은 잘 알려진 함수들에 대한 적분 테이블이다. $$ \begin{align} \int k dx = & \; kx + C \\ \int x^n dx = & \; \df..

지금까지 글에서 함수 아래에 놓인 넓이를 계산하기 위해 정적분을 이용했었다. 그리고 미분은 그래프의 기울기를 계산하기 위해 이용했었었다. 이번에 소개할 뉴턴과 라이프니츠가(따로) 발견한 미적분학의 기본정리(Fundamental Theorem of Calculus)는 전혀 관련이 없어보였던 미분과 적분은 서로 역연산 관계임을 알려주는 정리이다. 미적분학의 기본정리를 설명하기 위해 다음과 같이 정적분으로 정의된 함수 $g(x)$ 를 고려하자. $$ g(x) = \int_a^x f(t) \; dt $$ 여기서 $f$ 는 $[a,b]$ 에서 연속인 함수이고 $x \in [a,b]$ 이다. 그러면 아래 그림과 같이 $g(x)$ 는 $x$ 값에 따라 달라지는 $f$ 아래에 놓인 넓이를 나타내는 함수임을 알 수 있다..

이번에는 앞서 정의한 정적분의 여러가지 성질에 대해서 알아보자. 1. 적분 구간을 뒤집으면 반대부호가 된다. $$ \int_{\textcolor{red}{a}}^{\textcolor{blue}{b}} f(x) dx = -\int_\textcolor{blue}{b}^\textcolor{red}{a} f(x) dx $$ 더보기 적분의 정의에서 구간의 크기가 $\dfrac{b-a}{n}$ 였던 것이 $\dfrac{a - b}{n} = -\dfrac{b-a}{n}$ 로 바뀌므로 간단히 증명된다. 2. 구간의 크기가 $0$ 이면 적분 값은 $0$ 이다. $$ \int_\textcolor{red}{a}^\textcolor{red}{a} f(x) dx = 0 $$ 더보기 적분의 정의에서 구간의 크기가 $\dfrac{..