
넓이 계산하는 파트는 책만 읽어도 쉽게 이해 되므로 생략했다.
다음과 같은 물체를 살펴보자.

물체는 $x = a$ 부터 $x = b$ 까지의 범위에 분포해 있다.
임의의 점 $x$ 에서의 단면의 넓이를 $A(x)$ 라고 하자.
이 물체의 부피를 다음과 같이 $x$ 축에 평행하게 여러번 잘라 낸 부분 부피들의 합으로 근사시킬 수 있다.

예컨대, 7개 조각으로 나눈 위의 경우엔 부피 $V$ 는 다음과 같이 근사된다.
$$ V \approx \sum_{i = 1}^7 A(x_i) \cdot \Delta x$$
정적분에서 넓이를 구할 때처럼, 나눈 조각의 갯수가 많아질수록
실제 부피에 수렴하게 될 것으로 예상할 수 있다.
따라서 부피를 다음과 같이 정의한다.
부피의 정의 (정적분)
$S$ 가 $x = a$ 와 $x = b$ 사이에서 정의된 물체라고 하자.
$x$ 축과 수직한 면 $P_x$ 위에 놓인 $S$ 의 단면의 넓이가 $A(x)$ 라고 하고
이 때 $A(x)$ 가 연속함수이면 $S$ 의 부피 $V$ 는 다음과 같다.
$$ \textcolor{blueviolet}{V} = \lim_{n \to \infty} \sum_{i = 1}^n A(x_i^*) \Delta x = \textcolor{blueviolet}{\int_a^b A(x) \; dx}$$
즉, 부피를 계산하기 위해서는 다음의 스텝을 따라가면 된다.
1. 특정 축에 수직인 단면의 넓이를 나타내는 함수 $A(x)$ 를 찾고
2. 범위 내에서 정적분해준다.
예제 1
반지름이 $r$ 인 구의 부피가 $\dfrac{4}{3} \pi r^3$ 임을 보여라.
구의 중심을 원점으로 잡고 그림을 다음과 같이 그려보자.
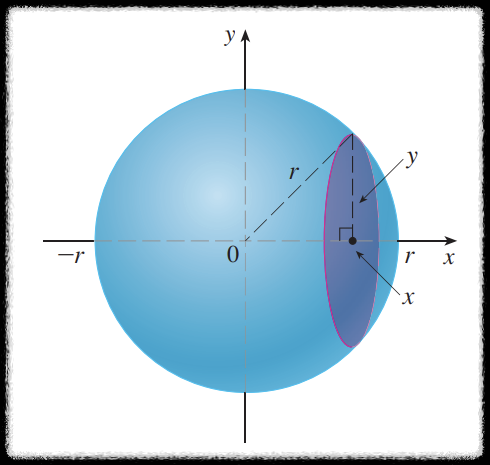
특정 $x$ 값에서의 단면의 넓이 $A(x)$ 는 피타고라스 정리에 의해 다음과 같다.
$$ A(x) = \pi y^2 = \pi(r^2 - x^2) $$
따라서 부피는 정의에 의해 다음과 같다.
$$ \begin{align} V = &\int_{-r}^r A(x) \; dx \\ = &\int_{-r}^r \pi(r^2 - x^2) \; dx \\ = &\left[ r^2x - \dfrac{x^3}{3} \right]_{-r}^r \\ = &\dfrac{4}{3}\pi r^3 \end{align} $$
물체가 특정 축에 대해 회전체인 경우도 있다.
이 것의 부피를 계산하는 법은 어렵지 않으므로 예제로 설명을 대체한다.
예제 2
$y = x^3$, $y = 8$, $x = 0$ 으로 둘러싸인 영역을 $y$ 축에 대해 회전시킨 물체의 부피를 구하라.
회전시키기 전의 영역은 다음과 같다.
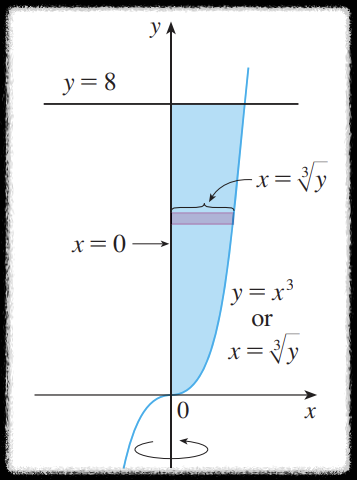
이 문제의 경우 단면을 $x$ 축에 수직으로 잡는 것 보다
$y$ 축에 수직인 단면을 잡아서 계산하는 것이 편해보인다.
$y = x^3$ 을 $x$ 에 대해 표현하면 $x = y^{\frac{1}{3}}$ 이므로
$y$ 축에 회전시킨 한 단면의 넓이는 $\textcolor{orange}{A(y)} = \pi x^2 = \textcolor{orange}{\pi y^{\frac{2}{3}}}$ 이다.
따라서 부피 식을 다음과 같이 세울 수 있다.
$$ \begin{align} V = &\int_{y=0}^{y=8} \textcolor{orange}{A(y)} \; dy \\ = &\pi \int_0^8 y^{\frac{2}{3}} \; dy \\ = &\pi \left[ \frac{3}{5}y^{\frac{5}{3}} \right]_0^8 \\ = &\dfrac{96}{5} \pi \end{align}$$
예제 3
카발리에리의 원리는 다음과 같다.
두 물체 $S_1$, $S_2$ 의 각 $x$ 값에서의 단면의 넓이가 같으면
두 물체의 부피는 같다.
이를 증명하고 이 원리를 이용해 다음 그림의 기울어진 실린더의 부피를 구하라
$x \in [a, b]$ 에서 정의된 연속함수 $A(x)$ 에 대해
단면의 넓이가 $A(x)$ 인 물체의 부피는 다음과 같음을 위에서 언급했다.
$$ V = \lim_{n \to \infty} \sum_{i = 1}^{n} A(x_i^*) \Delta x = \int_a^b A(x) \; dx $$
$S_1$ 의 단면을 $A_1(x)$ 라고 하고
$S_2$ 의 단면을 $A_2(x)$ 라고 하자.
정의에 의해 $S_1$ 의 부피는 다음과 같다.
$$V_1 = \int_a^b A_1(x) \; dx$$
그리고 $S_2$ 의 부피는 다음과 같다.
$$ V_2 = \int_a^b A_2(x) \; dx $$
이 때 $A_1(x) = A_2(x)$ 이므로, 이 결과를 $V_2$ 식에 대입하면 $V_1$ 식과 같다.
따라서 $V_1 = V_2$ 이다.
카발리에리 원리를 이용하면 기울어진 실린더의 부피는 원통의 부피와 같음을 알 수 있다.
왜냐하면 원통도, 기울어진 실린더도 높이 방향과 수직인 평면으로 자른 단면의 넓이가
$\pi r^2$ 로 같기 때문이다.
따라서 그림속 도형의 부피는 원통의 부피인 $\pi r^2 h$ 랑 같다.
위에서 살펴본 회전체의 부피 계산 방법은 원판 방법(Disk Method) 이였다.
회전체 부피를 계산하는 또 다른 방법으로 원통 껍질 방법(Cylindrical Shell Method)이 있다.
아래 그림과 같은 함수의 회전체는 위에서 보인 부피의 적분을 이용해 계산하기 까다롭다.
왜냐하면 $y$ 축에 대해 회전시킬 것이기 때문에 특정 $y$ 값에서의 $x$ 값들을 알아야하는데,
$y = 2x^2 - x^3$ 을 변형해서 $x = f(y)$ 꼴로 표현하기 힘들기 때문이다.
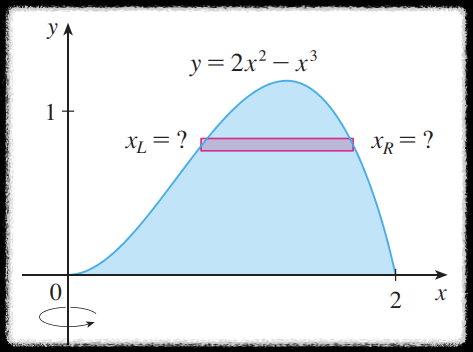
하지만 관점을 바꾸어 회전체의 부피를 다음처럼 원통형 껍질들의 합이라고 생각해보자.
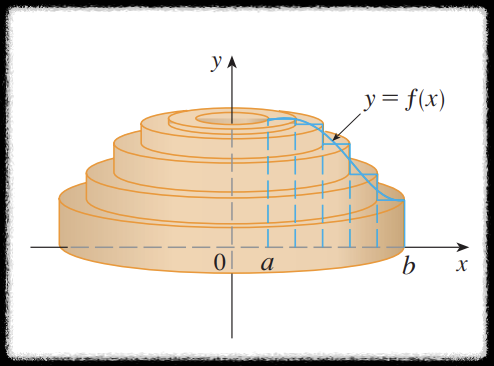
비유해서 표현하자면 휴지의 부피는 한바퀴 둘레를 만드는 휴지 부피들의 합이라고 생각할 수 있는 것과 같다.
이 방법을 이용하면 $y$ 축에 대한 단면의 넓이를 알 필요 없고
특정 반지름($x$)에서의 하나의 껍질의 부피만 알면 된다.
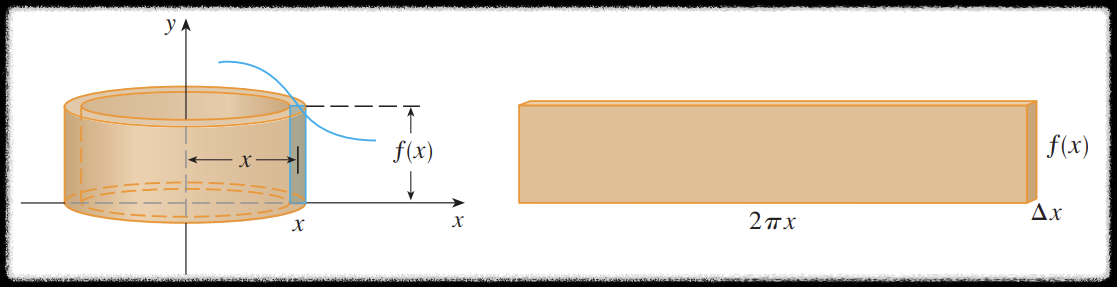
위 그림과 같이 회전축으로부터 거리가 $x$ 인 지점에서의 껍질은 펼쳐보면 오른쪽 그림과 같다.
이 직육면체의 부피는 $ \textcolor{skyblue}{\text{가로}} \times \textcolor{orange}{\text{세로}} \times \textcolor{limegreen}{\text{높이}} = \textcolor{skyblue}{2\pi x} \times \textcolor{orange}{\Delta x} \times \textcolor{limegreen}{f(x)}$ 이므로
전체 부피는 이 부피들의 합이고 따라서 다음과 같이 표현할 수 있을 것이다.
$$ V = \int \textcolor{skyblue}{2 \pi x} \textcolor{limegreen}{f(x)} \; \textcolor{orange}{dx} $$
원통 껍질 방법을 이용해 위의 문제를 해결해보자.
$$ \begin{align} V = &\int_0^2 \textcolor{skyblue}{2\pi x} \textcolor{limegreen}{(2x^2 - x^3)} \; \textcolor{orange}{dx} \\ = &2\pi \int_0^2 2x^3 - x^4 \; dx \\ = &\dfrac{16}{5}\pi \end{align}$$
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| [연습문제] 적분과 그 응용 (17~24) (0) | 2023.09.29 |
|---|---|
| 24. 함수의 평균값 (Average Value of a Function) (2) | 2023.09.28 |
| 22. 부분 적분 (Integration by Parts) (0) | 2023.09.28 |
| 21. 치환 적분 (Substitution Rule) (0) | 2023.09.24 |
| 20. 부정적분(Indefinite Integrals) (0) | 2023.09.24 |
