
$n$ 개의 값 $y_1, y_2, y_3, \cdots , y_n$ 의 평균은 다음과 같이 정의된다.
$$ y_{\text{avg}} = \dfrac{y_1 + y_2 + y_3 + \cdots + y_n}{n} = \dfrac{1}{n}\sum_{i = 1}^n y_i $$
무한히 많은 값을 갖는 함수에 대해서도 평균을 생각할 수 있다.
예를 들어 연속함수 $f(x) = x^2$ 의 $[0, 2]$ 에서의 평균은 다음과 같이 생각할 수 있다.
$x = 0$ 일 때 $y = f(0) = 0$
$x = 0.000...1$ 일 때 $y = f(0.000...1) = (0.000...1)^2$
$x = 0.000...2$ 일 때 $y = f(0.000...2) = (0.000...2)^2$
...
$x = 2$ 일 때 $y = f(2) = 2^2$
평균의 정의에 의해
위에 나열한 $y$ 값들의 합을 $\textcolor{skyblue}{\text{갯수} = n} $ 로 나누어주면 평균이다.
여기서 구간을 $\Delta x$ 크기의 $\textcolor{skyblue}{n}$ 개로 나누었다면 다음 식이 성립해야한다.
$$ \Delta x \times \textcolor{skyblue}{n} = \text{구간의 크기} = 2 $$
즉 $n$ 은 다음과 같고
$$ \textcolor{skyblue}{n} = \dfrac{2}{\Delta x} $$
평균의 정의를 이용하면 평균은 다음과 같다.
$$ y_{\text{avg}} = \dfrac{1}{\textcolor{skyblue}{n}} \sum_{i = 1}^n y_i = \dfrac{1}{\textcolor{skyblue}{2}} \sum_{i=1}^n y_i \textcolor{skyblue}{\Delta x} $$
함수의 값은 연속적이므로 $n \to \infty$ 극한을 취해주어야 한다.
즉 $y_{\text{avg}}$ 는 다음과 같이 적분으로 나타낼 수 있다.
$$ y_{\text{avg}} = \dfrac{1}{2} \int_{0}^{2} y(x) dx $$
위에서 얻은 결과를 살펴보면,
함수의 평균은 그 구간에서 적분한 값을 구간의 크기($=2$) 로 나누어준 것과 같음을 관찰할 수 있다.
이를 일반화 해보면 다음과 같다.
함수의 평균
구간 $[a, b]$ 에서 연속인 함수 $f$ 의 평균값은 다음과 같다.
$$ f_{\text{avg}} = \dfrac{1}{b-a} \int_{a}^{b} f(x) dx $$
일반적인 평균에서와 같은 느낌으로
함수의 평균의 의미는 구간 내에서 함수값들의 평균 높이를 나타낸다.
함수의 평균값이 이용된 정리를 하나 소개한다.
적분의 평균값 정리
$f$ 가 구간 $[a, b]$ 에서 연속이면 다음을 만족하는 수 $c \in (a, b)$ 가 존재한다.
$$ f(c) = f_{\text{avg}} = \dfrac{1}{b-a} \int_a^b f(x) \; dx $$
위 식을 다르게 표현하면 다음과 같다.
$$ \int_a^b f(x) \; dx = f(c)(b-a) $$
$g(x) = \int_a^x f(t) dt$ 라고 정의하자.
$f(t)$ 는 $[a, b]$ 에서 연속이므로 미적분학의 기본정리 1에 의해
$g(x)$ 는 $[a, b]$ 에서 연속이고 $(a, b)$ 에서 미분가능하며 $g'(x) = f(x)$ 를 만족한다.
따라서 $g(x)$ 는 평균값 정리에 의해 다음을 만족하는 $c \in (a, b)$ 가 존재한다.
$$ g(b) - g(a) = g'(c)(b - a) \; \textcolor{red}{\Longrightarrow} \; \int_a^b f(t) dt = f(c)(b-a)$$
(참고로 스튜어트 미적분학에서는 $c \in [a, b]$ 가 존재한다고 서술해놓았는데,
스튜어트에서는 이 정리를 증명하기 위해 중간값 정리를 이용하였기 때문이다.
"$c \in (a, b)$ 가 존재한다"가 "$c \in [a, b]$ 가 존재한다"보다 더 좁은 범위이므로 더 나은 증명법이다.)
이 정리의 의미는 아래 그림과 같이 함수 아래 놓인 넓이는
구간의 크기를 밑변, 함수의 평균값을 높이로 하는 직사각형의 넓이랑 같다는 것이다.

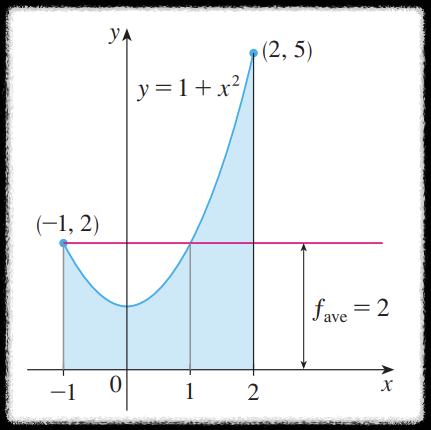
예제 1
구간 $ [-1, 2] $ 에서 함수 $f = 1 + x^2$ 가 평균값을 갖게 만드는 $x = c$ 값을 구하라.
$f$ 가 구간 내에서 연속이므로 적분의 평균값 정리에 의해
다음을 만족하는 $c \in (-1, 2)$ 가 존재한다.
$$ \int_{-1}^2 1 + x^2 \; dx = f(c)(2-(-1)) $$
좌변의 계산 결과는 $6$ 이므로
$$ 6 = (1 + c^2) \cdot 3 \; \textcolor{red}{\Longrightarrow} \; c^2 = 1 $$
$c \in (-1, 2)$ 이므로, $c = 1$ 일 때 함수가 평균값을 갖는다.
한편, $c = -1$ 일 때도 평균값을 갖는데,
그렇다고 해서 적분의 평균값 정리가 틀린 정리인 것은 아니다.
왜냐하면 $c \in (-1, 2)$ 가 하나 이상 존재함을 보여주는 정리지
모든 $c$ 값을 알려주는 정리인 것은 아니였기 때문이다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 벡터장과 스칼라장(Vector Fields and Scalar Fields) (0) | 2023.10.07 |
|---|---|
| [연습문제] 적분과 그 응용 (17~24) (0) | 2023.09.29 |
| 23. 적분을 이용한 부피 계산 (Volumes by Integration) (0) | 2023.09.28 |
| 22. 부분 적분 (Integration by Parts) (0) | 2023.09.28 |
| 21. 치환 적분 (Substitution Rule) (0) | 2023.09.24 |