23. 적분을 이용한 부피 계산 (Volumes by Integration)

넓이 계산하는 파트는 책만 읽어도 쉽게 이해 되므로 생략했다.

 

다음과 같은 물체를 살펴보자.

 

물체는 $x=a$ 부터 $x=b$ 까지의 범위에 분포해 있다.

임의의 점 $x$ 에서의 단면의 넓이를 $A(x)$ 라고 하자.

 

이 물체의 부피를 다음과 같이 $x$ 축에 평행하게 여러번 잘라 낸 부분 부피들의 합으로 근사시킬 수 있다.

 

예컨대, 7개 조각으로 나눈 위의 경우엔 부피 $V$ 는 다음과 같이 근사된다.

$$V\approx \sum _{i=1}^{7}A(x_i)\cdot \mathrm{\Delta }x$$

 

정적분에서 넓이를 구할 때처럼, 나눈 조각의 갯수가 많아질수록

실제 부피에 수렴하게 될 것으로 예상할 수 있다.

따라서 부피를 다음과 같이 정의한다.

 

부피의 정의 (정적분)

$S$ 가 $x=a$ 와 $x=b$ 사이에서 정의된 물체라고 하자.
$x$ 축과 수직한 면 $P_x$ 위에 놓인 $S$ 의 단면의 넓이가 $A(x)$ 라고 하고
이 때 $A(x)$ 가 연속함수이면 $S$ 의 부피 $V$ 는 다음과 같다.
$$V=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^{n}A(x_i^{\ast })\mathrm{\Delta }x={\int }_a^{b}A(x)dx$$

즉, 부피를 계산하기 위해서는 다음의 스텝을 따라가면 된다.

1. 특정 축에 수직인 단면의 넓이를 나타내는 함수 $A(x)$ 를 찾고

2. 범위 내에서 정적분해준다.

 

 

---

 

 

예제 1

반지름이 $r$ 인 구의 부피가 ${\displaystyle \frac{4}{3}}\pi r^3$ 임을 보여라.

구의 중심을 원점으로 잡고 그림을 다음과 같이 그려보자.

특정 $x$ 값에서의 단면의 넓이 $A(x)$ 는 피타고라스 정리에 의해 다음과 같다.

$$A(x)=\pi y^2=\pi (r^2-x^2)$$

따라서 부피는 정의에 의해 다음과 같다.

$$\begin{array}{rl}V=& {\int }_{-r}^{r}A(x)dx\\ =& {\int }_{-r}^r\pi (r^2-x^2)dx\\ =& {[r^{2}x-{\displaystyle \frac{x^3}{3}}]}_{-r}^r\\ =& {\displaystyle \frac{4}{3}}\pi r^3\end{array}$$

 

물체가 특정 축에 대해 회전체인 경우도 있다.

이 것의 부피를 계산하는 법은 어렵지 않으므로 예제로 설명을 대체한다.

 

예제 2

$y=x^3$, $y=8$, $x=0$ 으로 둘러싸인 영역을 $y$ 축에 대해 회전시킨 물체의 부피를 구하라.

회전시키기 전의 영역은 다음과 같다.

 

이 문제의 경우 단면을 $x$ 축에 수직으로 잡는 것 보다

$y$ 축에 수직인 단면을 잡아서 계산하는 것이 편해보인다.

 

$y=x^3$ 을 $x$ 에 대해 표현하면 $x=y^{\frac{1}{3}}$ 이므로

$y$ 축에 회전시킨 한 단면의 넓이는 $A(y)=\pi x^2=\pi y^{\frac{2}{3}}$ 이다.

따라서 부피 식을 다음과 같이 세울 수 있다.

$$\begin{array}{rl}V=& {\int }_{y=0}^{y=8}A(y)dy\\ =& \pi {\int }_0^8{y}^{\frac{2}{3}}dy\\ =& \pi {\left[\frac{3}{5}{y}^{\frac{5}{3}}\right]}_0^8\\ =& {\displaystyle \frac{96}{5}}\pi \end{array}$$

 

예제 3

카발리에리의 원리는 다음과 같다.
두 물체 $S_1$, $S_2$ 의 각 $x$ 값에서의 단면의 넓이가 같으면
두 물체의 부피는 같다.

이를 증명하고 이 원리를 이용해 다음 그림의 기울어진 실린더의 부피를 구하라

$x\in [a,b]$ 에서 정의된 연속함수 $A(x)$ 에 대해 

단면의 넓이가 $A(x)$ 인 물체의 부피는 다음과 같음을 위에서 언급했다.

$$V=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^{n}A(x_i^{\ast })\mathrm{\Delta }x={\int }_a^{b}A(x)dx$$

$S_1$ 의 단면을 $A_1(x)$ 라고 하고

$S_2$ 의 단면을 $A_2(x)$ 라고 하자.

정의에 의해 $S_1$ 의 부피는 다음과 같다.

$$V_1={\int }_a^b{A}_1(x)dx$$

그리고 $S_2$ 의 부피는 다음과 같다.

$$V_2={\int }_a^b{A}_2(x)dx$$

이 때 $A_1(x)=A_2(x)$ 이므로, 이 결과를 $V_2$ 식에 대입하면 $V_1$ 식과 같다.

따라서 $V_1=V_2$ 이다.

 

카발리에리 원리를 이용하면 기울어진 실린더의 부피는 원통의 부피와 같음을 알 수 있다.

왜냐하면 원통도, 기울어진 실린더도 높이 방향과 수직인 평면으로 자른 단면의 넓이가

$\pi r^2$ 로 같기 때문이다.

따라서 그림속 도형의 부피는 원통의 부피인 $\pi r^{2}h$ 랑 같다.

 

 

---

 

위에서 살펴본 회전체의 부피 계산 방법은 원판 방법(Disk Method) 이였다.

회전체 부피를 계산하는 또 다른 방법으로 원통 껍질 방법(Cylindrical Shell Method)이 있다.

 

아래 그림과 같은 함수의 회전체는 위에서 보인 부피의 적분을 이용해 계산하기 까다롭다.

왜냐하면 $y$ 축에 대해 회전시킬 것이기 때문에 특정 $y$ 값에서의 $x$ 값들을 알아야하는데,

$y=2x^2-x^3$ 을 변형해서 $x=f(y)$ 꼴로 표현하기 힘들기 때문이다.

 

 

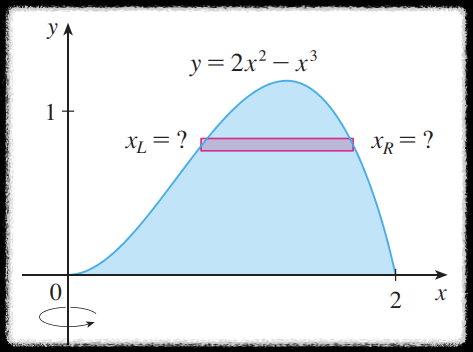
하지만 관점을 바꾸어 회전체의 부피를 다음처럼 원통형 껍질들의 합이라고 생각해보자.

 

 

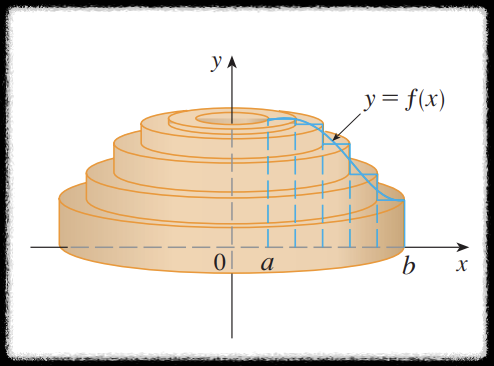
비유해서 표현하자면 휴지의 부피는 한바퀴 둘레를 만드는 휴지 부피들의 합이라고 생각할 수 있는 것과 같다.

이 방법을 이용하면 $y$ 축에 대한 단면의 넓이를 알 필요 없고

특정 반지름($x$)에서의 하나의 껍질의 부피만 알면 된다.

 

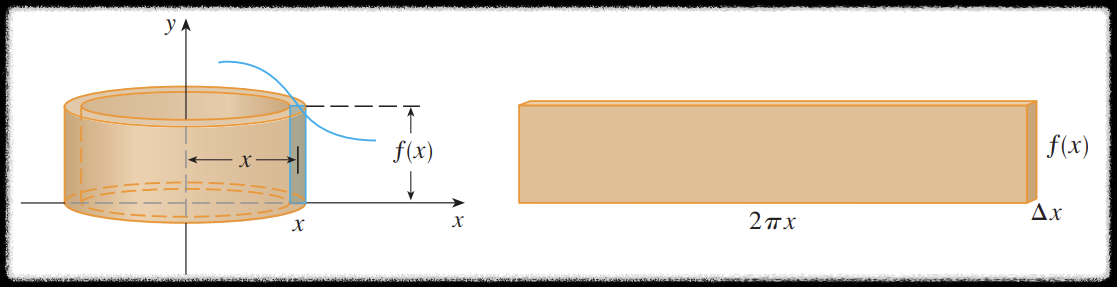
위 그림과 같이 회전축으로부터 거리가 $x$ 인 지점에서의 껍질은 펼쳐보면 오른쪽 그림과 같다.

이 직육면체의 부피는 $\text{가로}\times \text{세로}\times \text{높이}=2\pi x\times \mathrm{\Delta }x\times f(x)$  이므로

전체 부피는 이 부피들의 합이고 따라서 다음과 같이 표현할 수 있을 것이다.

$$V=\int 2\pi xf(x)dx$$

 

 

원통 껍질 방법을 이용해 위의 문제를 해결해보자.

$$\begin{array}{rl}V=& {\int }_0^{2}2\pi x(2x^2-x^3)dx\\ =& 2\pi {\int }_0^{2}2x^3-x^{4}dx\\ =& {\displaystyle \frac{16}{5}}\pi \end{array}$$