본 블로그의 미적분학 11번~16번 포스팅에 관한 연습문제이다.
1. 다음 문장들이 참인지 거짓인지 판단하고 거짓이라면 거짓인 이유를 서술하시오.
1-1) If $f'(c) = 0$, then $f$ has a local maximum or minimum at $c$.
False.
$f(x) = x^3$ 이면 $f'(0) = 0$ 이지만 $f$ 는 $0$ 에서 극대값도 극소값도 아니다.
왜냐하면 $0$ 을 기준 $x$ 값 좌우로 $f'(x) > 0$ 이므로 $f$ 는 $x=0$ 좌우에서 증가함수이고
따라서 국소적으로 최댓값 또는 최솟값을 가질 수가 없기 때문이다.
(13. 도함수 판정법의 1계 도함수 판정법 참조)
1-2) If $f$ has an absolute minimum at $c$, then $f'(c) = 0$
False.
$ f(x) = \begin{cases} -1 & \text{if } x = 0 \\ 1 & \text{if } x \neq 0 \end{cases}$ 이면 $f$ 는 $0$ 에서 최솟값을 갖지만
$f'(0)$ 가 정의되지 않으므로 $f'(0) = 0$ 이 아니다.
1-3) $f$ is continuous on $(a, b)$, then $f$ attains an absolute maximum value $f(c)$ and an absolute minimum value $f(d)$ at some numbers $c$ and $d$ in $(a, b)$.
False.
$f(x) = x^2$ 이고 구간이 $(-1, 1)$ 이라 하자.
그러면 $f(x)$ 는 $x = 0$ 에서 최솟값을 갖고 최댓값은 존재하지 않는다.
$x = 0$ 에서 최솟값을 갖는 것에 대한 설명 :
구간에 $x = -1, \; 1$ 을 추가해서 폐구간 $[-1, 1]$ 이라 하자. 폐구간 방법에 따르면,
임계수(Critical number)인 $x = 0$ 과 구간의 양 끝점인 $x=-1, \; 1$ 에서 최댓값 또는 최솟값을 갖는데,
$x = 0$ 일 때 최솟값이고 $x = -1, \; 1$ 일 때 같은 최댓값을 갖는다.
이제 $x = -1, \; 1$ 인 점을 제외시키면 최댓값은 존재하지 않고 최솟값만 남게된다.
1-4) If $f$ is differentiable and $f(-1) = f(1)$, then there is a number $c$ such that $| c | < 1$ and $f'(c) = 0$.
True.
$f$ 가 미분 가능하면 연속이므로(증명은 이 글 참조)
미분가능한 구간에 대해 따로 언급이 없는 이 함수 $f$ 는 전구간에서 미분가능하고 연속이다.
따라서 $[-1, 1]$ 에서 연속이고 $(-1, 1)$ 에서 미분가능하며, 조건에 의해 $f(-1) = f(1)$ 이므로
롤의 정리에 의해 $f'(c) = 0$ 인 $c \in (-1, 1)$ 가 존재한다.
$c \in (-1, 1)$ 은 $|c| < 1$ 과 동치이므로 증명 완료
1-5) There exists a function $f$ such that $f(x) < 0$, $f'(x) < 0$, and $f''(x)>0$ for all $x$.
$f(x)<0$ 이면 전 구간에서 음수인 함수라는 뜻이고
도함수 판정법에 의하면
$f'(x) < 0$ 이면 전 구간에서 감소, $f''(x) > 0$ 이면 전 구간에서 위로 오목이라는 뜻이다.
오목이면서 감소하는 함수는 $x \to -\infty$ 에서 $\infty$ 로 발산하므로 양수인 구간이 존재하게 된다.
따라서 조건을 만족하는 함수는 존재하지 않는다.
수식을 이용한 증명 :
평균값 정리에 의해 다음을 만족하는 $c \in (a, x)$ 가 존재한다.
$$ f(x) - f(a) = f'(c)(x-a) $$
한편, $f'' > 0$ 이므로 $f'$ 는 증가함수이고 따라서 $f'(a) < f'(c)$ 이다.
즉 $f(x) - f(a) = f'(c)(x-a) > f'(a)(x-a)$ 이고 정리하면 $f(x) > f(a) + f'(a)(x-a)$ 이다.
양변에 $-\infty$ 극한을 적용하면 우변은 $\infty$ 로 발산하므로 양수인 구간이 존재하게 된다.
1-6) If $f$ and $g$ are increasing on an interval $I$, then $f + g$ is increasing on $I$.
True.
$f, g$ 가 구간 $I$ 에서 증가한다는 말은 $I$ 에 속하는 임의의 $x_1 < x_2$ 에 대해
$$ \begin{cases} f(x_1) < f(x_2) \\ g(x_1) < g(x_2) \end{cases} $$
를 만족한다는 말이다.
둘을 더하면
$$ f(x_1) + g(x_1) < f(x_2) + g(x_2) $$
이므로 증가의 정의에 의해 참이다.
1-7) If $f$ is even, then $f'$ is even.
False.
반례 : $f(x) = x^2$ 이라하면 $f$ 는 우함수이지만 $f'(x) = x$ 로 기함수이다.
1-8) The most general antiderivative of $f(x) = x^{-2}$ is $$ F(x) = -\dfrac{1}{x} + C $$
True.
$\dfrac{d}{dx}\left( -\dfrac{1}{x} \right) = f$ 이므로 $-\dfrac{1}{x}$ 는 $f$ 의 역도함수이다.
또한 이 글의 정리에 의하면 $-\dfrac{1}{x}$ 에 상수를 더한 것이 가장 일반적인 역도함수 꼴임을 알 수 있다.
따라서 참이다.
2. $3x + 2\cos{x} + 5 = 0$ 가 오직 하나의 실근을 갖는다는 것을 증명하여라.
1. 실근이 존재함을 증명
$f(x) = 3x + 2\cos{x}$ 라고 하자.
$x = 0$ 이면 $f(0) = 5 > 0$
$x = -\pi$ 이면 $f(-\pi) = -3\pi + 3 < 0$ 이므로
중간값 정리에 의해 $f(c) = 0$ 이 되는 $c \in (-\pi, 0)$ 가 존재한다.
2. 근이 하나 뿐임을 증명
$f'(x) = 3 - 2\sin{x} > 0$ 이므로 $f(x)$ 는 전 구간에서 증가한다.
따라서 $x$ 축을 관통하는 점은 오직 $x = c$ 일 때 뿐이다.
3. 직선 $Ax + By + C = 0$ 와 점 $(x_1, y_1)$ 의 가장 가까운 거리 $d$ 는 다음과 같음을 증명하여라.
$$ d = \dfrac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}} $$
1. 벡터를 이용한 풀이
직선 $Ax + By + C$ 의 수직벡터는 $\mathbb{n} = <A, B>$ 이고
직선 위의 임의의 점 $(x, y)$ 에 대해 벡터 $\mathbb{r}$ 을 $\mathbb{r} = <x_1 - x, y_1 - y>$ 로 정의하면
직선과의 거리 $d$ 는 다음과 같다.
$$ \begin{align} d = |\text{comp}_{\mathbb{n}}{\mathbb{r}}| = &\left| \dfrac{ \mathbb{n} \cdot \mathbb{r} }{|\mathbb{n}|} \right| \\ = &\dfrac{|Ax_1 + By_1 \textcolor{limegreen}{- Ax - By}|}{\sqrt{A^2 + B^2}} \\ = &\dfrac{|Ax_1 + By_1 - \textcolor{limegreen}{(-C)}|}{\sqrt{A^2 + B^2}} \\ = &\dfrac{|Ax_1 + By_1 + C|}{\sqrt{A^2 + B^2}} \end{align}$$
2. 벡터를 쓰지 않는 풀이
직선 $Ax + By + C = 0$ 의 기울기는 $-\dfrac{B}{A}$ 인데 이와 수직인 기울기는 $\dfrac{A}{B}$ 이다.
기울기가 $\dfrac{A}{B}$ 이고 점 $(x_1, y_1)$ 을 지나는 직선의 방정식은 다음과 같다.
$$ y = \dfrac{A}{B}(x - x_1) + y_1 $$
이 직선과 처음의 직선 $Ax + By + C = 0 $ 를 연립하면 교점을 얻을 수 있는데,
이 교점과 점 $(x_1, y_1)$ 사이의 거리가 $d$ 가 된다.
계산은 복잡하므로 생략한다.
3. 또다른 풀이
2번 풀이에서 언급한 교점을 $(x, y)$ 라 하자. 그러면 $d^2$ 는 다음과 같다.
$$ d^2 = (x - x_1)^2 + (y - y_1)^2 $$
$(x, y)$ 는 직선 $Ax + By + C = 0$ 위의 점이므로 직선식을 대입할 수 있다.
$$Ax + By + C = 0 \Longrightarrow x = -\dfrac{B}{A}y - \dfrac{C}{A}$$
로 변형한 후 대입하면 $y$ 에 대한 2차방정식이 나온다.
미분을 이용하여 최솟값을 구하면 되는데, 역시 계산이 복잡하므로 생략한다.
현재 단원까지는 벡터를 배우지 않아서 복잡한 계산을 하지만
후에 벡터를 공부하면 1번 풀이와 같이 간단하게 계산해낼 수 있다.
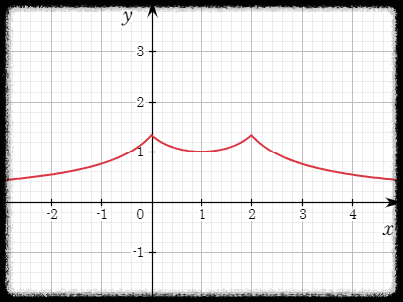
4. Find the absolute maximum value of the function
$$ f(x) = \dfrac{1}{1 + |x|} + \dfrac{1}{1 + |x - 2|} $$
절댓값이 $0$ 일 때 기준으로 식이 달라지므로
$x = 0, \; x = 2$ 를 기준으로 식을 나눠서 생각해야 한다.
$$ f(x) = \begin{cases} \dfrac{1}{1 - x} + \dfrac{1}{3 - x} \quad \text{if } x < 0 \\ \dfrac{1}{1 + x} + \dfrac{1}{3-x} \quad \text{if } 0 \le x <2 \\ \dfrac{1}{1 + x} + \dfrac{1}{x-1} \quad \text{if } 2 \le x \end{cases}$$
정리하면
$$f(x) = \begin{cases} \dfrac{-2(x-2)}{(x-1)(x-3)} \quad \text{if } x < 0 \\ \dfrac{-4}{(x+1)(x-3)} \quad \text{if } 0 \le x <2 \\ \dfrac{2x}{(x+1)(x-1)} \quad \text{if } 2 \le x \end{cases} $$
한편, $f(1+x) = f(1-x)$ 이므로 $f$ 는 $x = 1$ 에 대칭이다.
편의를 위해 $x>1$ 일 때만 계산하자.
$$f'(x) = \begin{cases} \dfrac{8(x-1)}{(x+1)^2(x-3)^2} \textcolor{red}{> 0} \quad \text{if } 1 \le x < 2 \\ \dfrac{-2(x^2 + 1)}{(x+1)^2(x-1)^2} \textcolor{red}{< 0} \quad \text{if } x > 2 \end{cases}$$
$x = 2$ 기준으로 왼쪽에서 증가하다가 오른쪽에서 감소하므로 $x = 2$ 에서 극댓값을 갖는다.
반으로 자른 구간의 끝 점인 $x = 1$ 에서의 함숫값은 $f(1) = 1$ 이고 $f(2) = \dfrac{4}{3}$ 이며
$x>2$ 에서는 감소하며 더 이상 극값이 없으므로 $f$ 의 최댓값은 $f(2) = \dfrac{4}{3}$ 이다.
그래프는 다음과 같다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 18. 정적분의 성질 (Properties of Definite Integral) (0) | 2023.09.24 |
|---|---|
| 17. 넓이 문제와 정적분 (Area problem and Definite Integrals) (0) | 2023.09.23 |
| 16. 역도함수(Antiderivative) (0) | 2022.12.22 |
| 15. 미분을 이용한 곡선 그리기 (2) | 2022.01.20 |
| 14. 점근선 (Asymptote) (0) | 2022.01.07 |