이전 포스팅에서 함수 \(f\)의 고정된 값 \(a\) 에서의 미분계수에 대해 다뤘고 다음과 같은 식임을 알았다.
$$ f'(a) = \lim_{h \to 0} \dfrac{f(a + h) - f(a)}{h} $$
그리고 자연스럽게 고정된 점이 아닌 임의의 점 \(x\) 에서의 미분계수도 생각해볼 수 있을것이다.
다음과 같이 \(a\) 대신에 \(x\) 를 대입함으로써 이를 구할 수 있다.
$$ f'(x) = \lim_{h \to 0} \dfrac{f(x+h) - f(x)}{h} \tag{f의 도함수} $$
위 식을 잘 보자.
정의역의 \(x\) 라는 값이 들어가면 \(x\) 점의 미분계수가 되어
\(\lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}\) 라는 값이 튀어 나오는 것이 마치 함수와 같다.
즉 \(\lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}\) 극한이 존재하기만 하면
이 때의 \(x\) 값들을 모두 \(f'(x)\) 에 대응시킬 수 있고
\(f'\) 를 \(f\) 의 도함수라고 부르는 새로운 함수로 정의할 수 있게 된다.
도함수를 나타내는 다른 표현으로는 \(y = f(x)\) 일 때
\(f'(x) = \dfrac{dy}{dx} = \dfrac{df}{dx} = \dfrac{d}{dx}f \) 등이 있다.
이런 방식의 표현을 라이프니츠식 표기법이라고 하고
다가올 포스팅에서 서술할 연쇄법칙을 적용할 때 편리한 표현방식을 제공해준다.
도함수의 직관적인 의미는 무엇일까?
\(x=a\) 에서의 미분계수가 그 점에서의 기울기임을 저번 포스팅에서 확인하였다.
따라서 임의의 점에서의 기울기에 대한 함수가 도함수라고 할 수 있을것이다.
다음 그림을 보며 도함수의 의미에 대해 감을 잡아보자.

위 그림에서 두 그래프 중 위쪽의 그래프는 원함수(원래 함수) \(f(x)\) 이고 아래의 그래프는 도함수 \(f'(x)\) 를 나타내었다.
원함수에서 점 \(A\)의 이전 구간에는 곡선이 점점 내려가므로 기울기가 음수이다.
그리고 같은 구간에서 도함수 \(f'\) 가 0보다 아래에 있는것을 확인할 수 있다.
원함수에서 점 \(A\) 와 \(B\) 사이의 구간에서는 곡선이 점점 올라가므로 기울기가 양수이다.
그리고 같은 구간에서 도함수 \(f'\) 가 0보다 위에 있는것을 확인할 수 있다.
원함수에서 점 \(A, B, C\) 의 순간에서는 곡선이 증가하지도 감소하지도 않는다. 따라서 기울기가 0이고
같은 위치에서 도함수의 값이 0임을 확인할 수 있다.
원함수의 점 \(P\) 에서 기울기가 약 \(\frac{3}{2}\) 라고 되어있다.
같은 위치에서 도함수의 값이 약 \(\frac{3}{2} = 1.5\) 임을 확인할 수 있다.
다른 구간에도 같은 방식으로 생각할 수 있다.
임의의 구간에서 도함수는 항상 존재할까? 그렇지 않다.
위에서 언급하였듯이 \(\lim\limits_{h \to 0} \dfrac{f(x+h) - f(x)}{h}\) 의 극한이 존재 하는 곳에서만 정의된다.
다음 예제를 보자
\(Q1.) f(x) = \sqrt{x}\) 일 때 \(f\) 의 도함수를 구하고 정의역을 구하라.
풀이
도함수의 정의에 의해
$$ \begin{align} f'(x) = &\lim_{h \to 0} \dfrac{f(x+h) - f(x)}{h} \\ = &\lim_{h \to 0} \dfrac{\sqrt{x+h} - \sqrt{x}}{h} \\ = &\lim_{h \to 0} \dfrac{\sqrt{x+h} - \sqrt{x}}{h} \cdot \dfrac{\sqrt{x+h} + \sqrt{x}}{\sqrt{x+h} + \sqrt{x}} \\ = &\lim_{h \to 0} \dfrac{(x+h) - x}{h(\sqrt{x+h} + \sqrt{x})} \\ = &\lim_{h \to 0} \dfrac{1}{\sqrt{x+h} + \sqrt{x}} \\ = &\dfrac{1}{2\sqrt{x}} \end{align} $$
\(x < 0\) 이면 \(\sqrt{x}\) 가 정의가 안되므로 \(f'(x)\) 극한이 존재하지 않게 된다.
또 $x = 0$ 인 경우에는 분모의 $\sqrt{x}$ 가 $0$ 이 되므로 이 때도 극한이 존재하지 않는다.
따라서 \(x < 0 \)에서 도함수가 정의되고
\(f'(x) = \dfrac{1}{2\sqrt{x}}\) 이다.
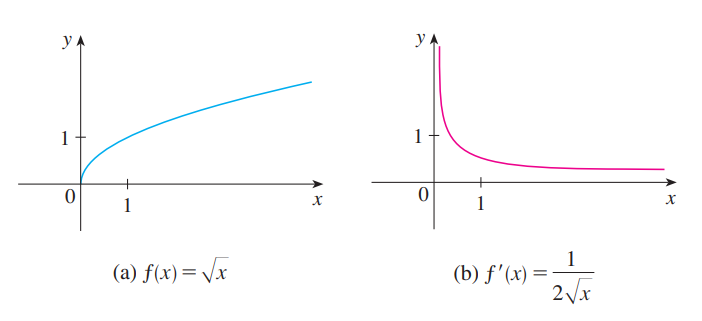
위 예시에서 보았듯이 항상 모든 구간에서 미분계수가 존재하는것이 아니다.
\(x=a\) 에서의 미분계수 \(f'(a)\) 가 존재한다면 이를 다른 말로 \(f\) 는 \(x = a\) 에서 미분가능하다 라고 표현한다.
그리고 열린 구간 \((a, b)\) 에서 미분 계수가 모조리 존재한다면 \(f\) 는 \((a, b)\) 에서 미분가능하다 라고 표현한다.
\((a, \infty), (-\infty, a), (-\infty, \infty)\) 에서도 마찬가지이다.
(닫힌구간이 아니라 열린구간으로 표현한 이유)
\(x=a\) 에서 미분계수가 존재하려면 다음의 극한이 존재해야 한다.
$$ \lim_{x \to a} \dfrac{f(x) - f(a)}{x-a} \text{ 또는 } \lim_{h \to 0} \dfrac{f(a+h) - f(a)}{h} $$
우극한 좌극한 모두 존재할 때 극한이 존재한다 라고 표현했음을 상기하자.
원래 함수 \(f\) 의 정의역이 닫힌 구간 \([a, b]\) 으로 주어졌다고 가정하자.
그리고 \(x = a\) 일 때의 미분계수인 \(\lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x-a}\) 를 계산하려고 해보자.
이 함수의 \(x<a\) 인 구간에서는 함수가 정의가 안되므로
좌극한을 계산하기 위한 \(\lim\limits_{x \to a^{-}} \dfrac{f(x) - f(a)}{x-a}\) 의 식 중
분자의 \(f(x)\)는 말이 안되는 식이 된다.
따라서 좌극한이 존재하지 않고 \( \lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x-a} \) 의 극한은 존재하지 않는다.
\(x = b\) 에서의 우극한도 비슷한 방식으로 존재하지 않고 따라서 극한도 존재하지 않는다.
이러한 이유로 닫힌 구간으로 주어진 정의역 \([a, b]\)에서는 아무리 미분 가능한점이 많아도
열린 구간 \((a, b)\) 보다 더 많을 수는 없다.
따라서 편리성을 위해 일반적으로 열린구간으로 표현한것일 뿐이다.
정의역보다 작은 정의역 안에 포함된 구간이라면 닫힌구간에서 미분가능하다는 표현도 가능하다.
\(\text{ex) }\) \(f\) 가 \((-1, 5)\) 에서 미분 가능하다면 \(f\) 는 \([0, 3]\) 에서 미분 가능하다고 표현할 수 있다.
4번째 포스팅 여기(링크) 에서 함수의 성질 중 연속성에 대해 다루었다.
그리고 미분가능성 역시 함수의 성질이라 할 수 있다.
다음 정리는 이 두 가지 성질이 어떻게 연결되어 있는지 보여준다.
정리
$f$ 가 $a$ 에서 미분가능하면 $f$ 는 $a$ 에서 연속이다.
증명
\(f\) 가 \(x=a\) 에서 미분가능하다는 말은 다음의 극한이 존재한다는 말이다.
$$ f'(a) = \lim_{x \to a} \dfrac{f(x) - f(a)}{x-a}$$
그리고
\(f\) 가 \(x = a\) 에서 연속이라는 말은 다음이 성립한다는 말이다.
$$ \lim_{x \to a} f(x) = f(a) $$
이제 이 둘을 연결시켜 보이면 된다.
먼저 \(\lim\limits_{x \to a} [f(x) - f(a)] = 0\) 임을 보이자.
\(\lim\limits_{x \to a} \dfrac{f(x) - f(a)}{x-a} = f'(a)\) 로 수렴함이 주어져있다.
또 한편 $\lim\limits_{x \to a} (x-a) = 0$ 이므로 수렴한다. 따라서 다음이 성립할 것이다.
$$ \begin{align} \lim_{x \to a} [f(x) - f(a)] = &\lim_{x \to a} \left[ \dfrac{f(x) - f(a)}{x-a} \cdot (x-a) \right] \\ = &\left[ \lim_{x \to a} \dfrac{f(x) - f(a)}{x-a} \right] \cdot \left[ \lim_{x \to a} (x - a) \right] \tag{극한법칙} \\ = &f'(a) \cdot 0 \\ =& 0\end{align}$$
그리고 \(\lim\limits_{x \to a} f(x) = \lim\limits_{x \to a} [f(x) - f(a)] + f(a)\) 인데
\(\lim\limits_{x \to a} [f(x) - f(a)] = 0\) 으로 수렴함을 위에서 보였고
\(\lim\limits_{x \to a} f(a) = f(a)\) 으로 역시 수렴하므로 극한법칙에 의해
$$ \begin{align} \lim_{x \to a} f(x) = &\lim_{x \to a} [f(x) - f(a)] + f(a) \\ = &\lim_{x \to a} f(x) - f(a) + \lim_{x \to a} f(a) \\ = &0 + f(a) \\ = &f(a) \end{align}$$
\(\lim\limits_{x \to a} f(x) = f(a)\) 임을 보였으므로 \(f\) 는 \(x = a\) 에서 연속이다.
참고로 고교 수학에서 "미분가능하려면 연속이어야 한다" 라고 배운 경우가 있을텐데
맞는 말이기는 하다만 이것만 기억을 해서 마치 미분가능성의 정의에 연속이 포함된 것처럼 오해할 수 있다.
다시 정의를 보면 알겠지만 \(f\) 의 미분가능성의 정의엔 \(f\) 의 연속성 개념이 포함되어 있지 않다.
그렇다면 왜 그런 말이 나온것일까?
위에서 보인 정리에 의해서 (\(f\) 가 미분가능하면 / \(f\)는 연속이다.) 가 참이다.
"\(f\) 가 연속이다" 는 "\(f\) 가 미분가능하다"의 필요조건인것이다.
따라서 \(f\) 가 미분가능하려면 우선 \(f\) 가 연속이어야 한다는 말도 되는것이다.
비유하자면
(펭수가 펭귄이면 / 펭수는 동물이다.) 에서 펭수가 펭귄이려면 우선 펭수가 동물이어야 하는것은 당연한 일이다.
펭수가 우선 동물이어야 펭귄인지 아닌지 따져볼 수 있는 것이다.
함수 \(f\)의 도함수 \(f'\) 가 있듯이 함수 \(f'\)의 도함수 \(f''\) 도 존재한다.
도함수를 정의했던 방법과 같은 방식으로 \(f\) 대신에 \(f'\) 를 넣어 다음과 같이 정의된다.
$$ f''(a) = \lim_{h \to 0} \dfrac{f'(a + h) - f'(a)}{h} $$
이를 함수 \(f\) 의 2계도함수 라고 부르고
\(y = f(x)\) 으로 주어질 때 라이프니츠식 표기법으로는 다음과 같이 적는다.
\(\dfrac{d}{dx} \left( \dfrac{dy}{dx} \right) = \dfrac{d^{2}y}{dx^{2}} \)
마찬가지의 방법으로 3계도함수 또는 그 이상의 고계도함수도 정의할 수 있다.
이전글 : 5. 함수의 기울기와 미분계수 (Slope and Derivative of a function)
다음글 : 7. 미분 공식 (Differentiation Formulas)
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 8. 연쇄 법칙과 증명 (Chain Rule) (10) | 2021.01.19 |
|---|---|
| 7. 미분 공식 (Differentiation Formulae) (0) | 2021.01.12 |
| 5. 함수의 기울기와 미분계수 (Slope and Derivative of a function) (0) | 2021.01.06 |
| [연습문제] 극한, \(\epsilon - \delta\)논법, 연속 (1~4) (0) | 2021.01.04 |
| 4. 함수의 연속과 중간값 정리 (Continuity and Intermediate Value Theorem) (0) | 2021.01.03 |