8. 연쇄 법칙과 증명 (Chain Rule)

 

7. 미분 공식 (Differentiation Formulas)
에서 함수의 합에 대한 미분법칙, 곱에 대한 미분법칙, 차에 대한 미분법칙 등등 
함수들의 대수적인 연산에 대한 미분법칙에 대해 알아보았었다.

이번 포스팅에서는 합성함수에 대한 미분법칙을 다루려고 한다.

 

참고로 이번 글은 평소보다 부연설명을 더욱 자세히 적어서

초보자들이 잘 이해 못하는 점들을 모두 해결해주는데 집중하였다.
핵심만 찾고자 한다면 전공책을 보는것이 나을 수도 있다.

---

 

미분계수는 그 점에서의 ${\displaystyle \frac{y순간증가율}{x순간증가율}}$ 로 정의되었었고 라이프니츠식 표기법으로 ${\displaystyle \frac{dy}{dx}}$ 로 표현된다는 것을
5. 함수의 기울기와 미분계수, 6. 도함수와 미분가능성 에서 알아보았었다.

 

 

이제 합성함수 $F(x)=f(g(x))=(f\circ g)(x)$ 를 살펴보자. $f,g$는 모두 미분 가능하다고 가정한다.

$f$ 의 내부 변수인 $g$ 가 변할 때 $f$ 의 변화율을 보고자 한다면 ${\displaystyle \frac{df}{dg}}$ 를 생각해볼 수 있을것이다.

$g$ 의 내부 변수인 $x$ 가 변할 때 $g$ 의 변화율을 보고자 한다면 ${\displaystyle \frac{dg}{dx}}$ 를 생각해볼 수 있을것이다.

 

 

한편 $F$의 입장에서 $x$가 변할 때의 변화율을 보고자 한다면 ${\displaystyle \frac{dF}{dx}}$ 을 생각해볼 수 있는데,

이 미분계수를 분수처럼 본다면 다음과 같이 두 미분계수의 곱으로 적을 수 있을것처럼 보인다.

$$\begin{array}{rl}{\displaystyle \frac{dF}{dx}}=& {\displaystyle \frac{df}{dx}}\\ =& {\displaystyle \frac{df}{dg}}\cdot {\displaystyle \frac{dg}{dx}}\end{array}$$

 

사실 여부를 확인하기 위해 다음과 같은 예를 들어보자.

$F(x)=(3x+1{)}^2$ 의 $x=2$ 에서의 미분계수는 무엇일까?

 

합성함수의 미분법을 제쳐두고 원래 방법대로 먼저 계산해보자.

$F(x)=(3x+1)\cdot (3x+1)$ 이므로 곱의 미분을 이용하면
$F^{\prime }(x)=(3)\cdot (3x+1)+(3x+1)\cdot (3)=6(3x+1)$ 이므로
$F^{\prime }(2)=6\cdot 7=42$

 

한편 $f(x)=x^2,g(x)=3x+1$ 이라 하면

$F(x)$ 는 $F(x)=f(g(x))$ 인 합성함수로 볼 수 있다.

 

위에서 추측한대로라면

$x=2$ 일 때의 $g(x)$ 의 미분계수인 $g^{\prime }(2)$ 와 
$x=2$ 일 때의 $f(g)$ 의 미분계수 ($f(x)$ 가 아니다!)
즉 $g=g(2)=7$ 일 때의 $f^{\prime }(g)=$ $f^{\prime }(7)$ 의 곱인 $[f^{\prime }(7)\cdot g(2)]$ 가 $F^{\prime }(2)$ 랑 같은 값이 나와야 한다.

 

그리고 $f^{\prime }(7)=14,g^{\prime }(2)=3$ 이고 이들의 곱은 $42$ 이므로 위에서 구한 $F^{\prime }(2)$와 같음이 확인된다.

따라서 위의 추측은 타당해보이고 실제로도 타당하며 아래에서 증명할 것이다.

이처럼 합성함수의 미분을 두 함수의 증가율의 곱으로 표현하는 법칙을 연쇄법칙이라 부른다.

 

 

 

 

연쇄법칙

$f$ 와 $g$ 가 모두 미분가능하고 $F=f\circ g$ 가 $F(x)=f(g(x))$ 로 정의된 합성함수라면,
$F$ 는 $x$ 에서 미분 가능하고, $F^{\prime }$ 는 다음과 같은 곱으로 주어진다.$$F^{\prime }(x)=f^{\prime }(g(x))\cdot g^{\prime }(x)$$

라이프니츠 기호로 나타내면, $y=f(u)$ 와 $u=g(x)$ 가 모두 미분가능한 함수일 때 다음이 성립한다.
$${\displaystyle \frac{dy}{dx}}={\displaystyle \frac{dy}{du}}\cdot {\displaystyle \frac{du}{dx}}$$

 

 

 

 

이 법칙의 완벽한 증명을 적기 전에 다음과 같이 생각하여보자.

완벽한 증명만 바로 보고 싶다면 넘어가도 되지만, 한 번 쯤은 보고 넘어가자.

 

---

불완전한 증명

사전 작업

일반적으로 $y=f(x)$인 함수에서 $x$ 의 변화량 $\mathrm{\Delta }x$ 에 대해

$x$ 가 $\mathrm{\Delta }x$ 변할 때 $y$ 의 변화량을 $\mathrm{\Delta }y$ 라고 하면
$\mathrm{\Delta }y=f(x+\mathrm{\Delta }x)-f(x)$ 라고 할 수 있다.

(미분계수의 정의 설명하는 과정에서 $y변화량=f(x+h)-f(x)$ 였음을 떠올려보라)

마찬가지로 $u=g(x)$ 로 표현되는 함수에서는 $$\mathrm{\Delta }u=g(x+\mathrm{\Delta }x)-g(x)$$

또 $y=f(u)$ 에서는 다음이 성립한다.
$$\mathrm{\Delta }y=f(u+\mathrm{\Delta }u)-f(u)$$

 

 

본론

이것을 이용해 원하는 연쇄법칙을 유도해보자.

$\mathrm{\Delta }u\ne 0$ 이라면 다음이 성립할것이다.

$$\begin{array}{rl}{\displaystyle \frac{dy}{dx}}=& \underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}\\ =& \underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\cdot {\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\end{array}$$ 

 

여기서

$\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}$ 가 수렴하고 $\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}$ 도 수렴한다면 극한법칙에 의해 다음과 같이 분리될 것이다.

$$\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\cdot {\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}=\left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\right]\cdot \left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\right]$$

 

$u=g(x)$가 미분가능하므로 오른쪽 부분인 다음이 수렴하는것은 당연하다.

$$\left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\right]$$

이제 왼쪽 부분인 다음의 식도 수렴하는지 살펴보자.

$$\left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\right]$$

 

우선 $y=f(u)$가 미분가능하므로 다음이 수렴한다.

$$\underset{\mathrm{\Delta }u\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}$$

 

그리고 $u=g(x)$ 가 미분가능하므로 $g(x)$ 는 연속이다. (미분가능하면 연속이라는 정리에 의해)

따라서 연속의 정의에 의해 $\mathrm{\Delta }x\to 0$ 이면 $\mathrm{\Delta }u=g(x+\mathrm{\Delta }x)-g(x)$ 는 $0$으로 수렴해야한다.

즉, $\mathrm{\Delta }x\to 0$ 이면 $\mathrm{\Delta }u\to 0$ 라는 말이고 이는 다음 식처럼 $\mathrm{\Delta }x\to 0$ 일 때도 수렴함을 보여준다.
$$\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}$$


극한법칙이 적용될 수 있다는것을 알았으니 원래 하던 계산으로 돌아오면
$$\begin{array}{rl}{\displaystyle \frac{dy}{dx}}=& \underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}\\ =& \underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\cdot {\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\\ =& \left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\right]\cdot \left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\right]\\ =& \left[\underset{\mathrm{\Delta }u\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}\right]\cdot \left[\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }u}{\mathrm{\Delta }x}}\right]\\ =& {\displaystyle \frac{dy}{du}}\cdot {\displaystyle \frac{du}{dx}}\end{array}$$ 

---

 

 

이로써 연쇄법칙이 $\mathrm{\Delta }u\ne 0$ 인 경우에 한정해서 증명되었다.

이는 고등학교 교과서에 나와있는 증명법(에다가 부연설명을 잔뜩 넣었지만)인데, 완벽한 증명이라고 할 수는 없지만 대충 옳은 법칙임을 암시해주는 역할은 한다.
$\mathrm{\Delta }u\ne 0$ 조건을 뺀 증명이 완벽하지 않은 이유는 다음과 같다.

$y=f(u)$ 가 어떤 식으로 주어져있다고 가정하고
$u=g(x)$ 가 다음과 같이 정의되었다고 해보자
$$u=g(x)=\{\begin{array}{ll}{x}^2\sin \left({\displaystyle \frac{1}{x}}\right)& (x\ne 0)\\ 0& (x=0)\end{array}$$

참고로 미분계수의 정의로 직접 계산을 해보면 알겠지만 이 함수는 $0$ 에서도 미분 가능하다.

 

이 함수는 그림과 같이 $x=0$ 근처에서 무한히 진동하며 $u=0$ 을 무한히 많이 지난다.

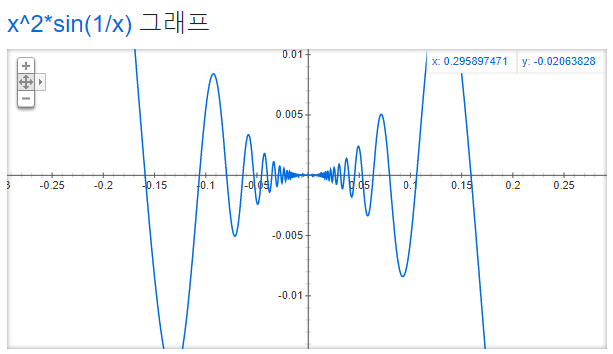
합성함수 $y=f\circ g$ 의 $x=0$ 에서의 미분계수를 구하고자 하여 $\mathrm{\Delta }u=g(0+\mathrm{\Delta }x)-g(0)$ 으로 정의한 후

위에서 언급한 증명법을 따라가는 도중 $\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}$ 를 구하려고 할 때 문제가 생긴다. 

왜냐하면 $\mathrm{\Delta }x$ 를 아무리 작게 설정해도 $0$ 에 더욱 접근시키면서
$g(0+\mathrm{\Delta }x)=0=g(0)$ 가 되게 하는 $\mathrm{\Delta }x$ 값이 생기기 때문에 

$\mathrm{\Delta }u=0-0=0$ 이 되는 경우가 항상 존재하고 따라서 $\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }u}}$ 가 정의가 되지 않는다.

고교과정에서 나오는 단순한 함수들에 대해서는 별 문제가 되지 않지만 이런 함수들이 존재하기 때문에 위의 증명법은 완벽하다고 할 수 없다.

 

 

 

연쇄법칙은 $\mathrm{\Delta }u=0$ 가 되는 경우에도 상관없이 성립하는 법칙이다.
이를 위해서는 위의 증명 방식처럼 $\mathrm{\Delta }u$ 가 분모에 들어가서 $0$으로 나누게 되는 경우를 만들면 안된다.

본격적으로 증명으로 들어가기 이전에 그런 상황을 방지하기 위한 유용한 표현법을 하나 알아보고 가자.

 

---

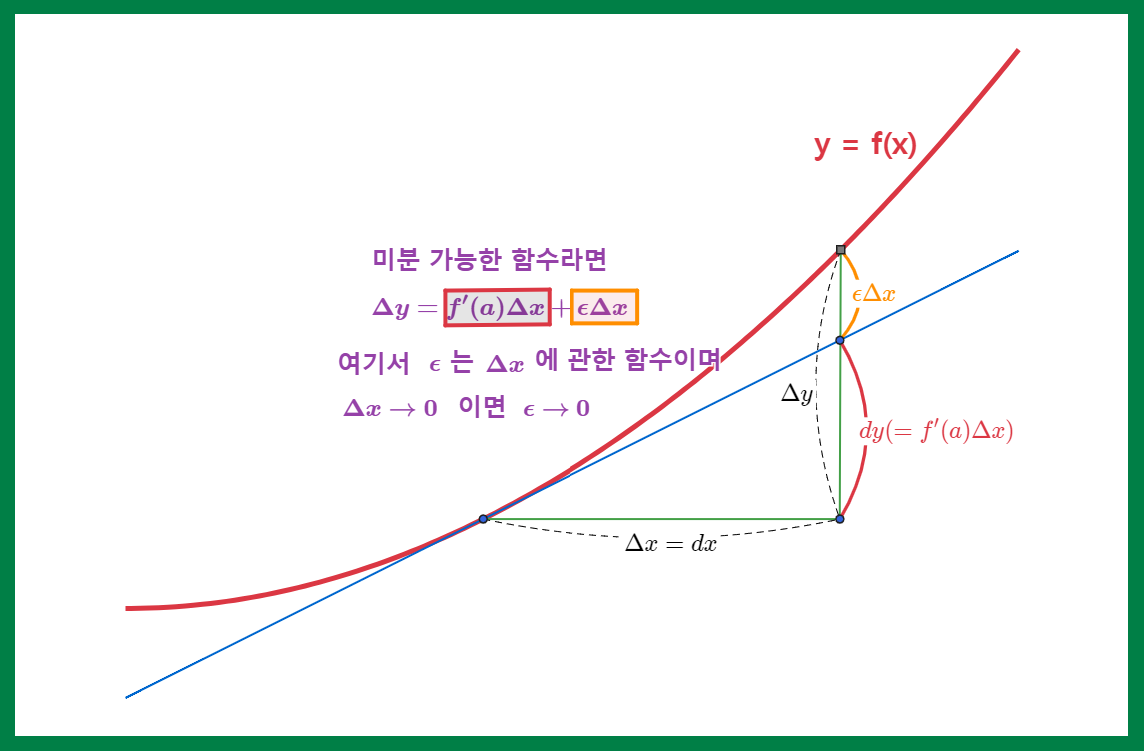
$y=f(x)$ 꼴로 표현되는 함수가 $x=a$ 에서 미분 가능하다면
$y$ 의 증분이 $\mathrm{\Delta }y=f(a+\mathrm{\Delta }x)-f(a)$ 로 정의될 때, 도함수의 정의에 의해 다음의 극한이 존재해야 한다.
$$f^{\prime }(a)=\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}$$

 

그리고 $\mathrm{\Delta }x\ne 0$ 일 때 $ϵ$ 이 ${\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}$ 와 ${\displaystyle \frac{dy}{dx}}=f^{\prime }(a)$ 의 차로 정의된다면 다음이 성립한다.
$$\underset{\mathrm{\Delta }x\to 0}{lim}ϵ=\underset{\mathrm{\Delta }x\to 0}{lim}[{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}-f^{\prime }(a)]=f^{\prime }(a)-f^{\prime }(a)=0$$ 따라서 $\mathrm{\Delta }x\to 0$ 이면 $ϵ\to 0$ 이 성립하게 된다.

$\mathrm{\Delta }x=0$ 일 때는 $ϵ=0$ 이라고 정의하면 $ϵ$ 은 $\mathrm{\Delta }x$ 에 대해 연속인 함수가 된다.

 

한편 $ϵ={\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}-f^{\prime }(a)$ 였으므로 이 식을 변형하면 다음을 얻는다.

$$\begin{array}{}\text{(식 1)}& \mathrm{\Delta }y=f^{\prime }(a)\mathrm{\Delta }x+ϵ\mathrm{\Delta }x\end{array}$$

 

정리하면, $y=f(x)$ 꼴로 표현되는 함수가 $x=a$ 에서 미분가능하다면 다음과 같은 식으로 표현될 수 있다.

$$\begin{array}{rlr}\mathrm{\Delta }y=f^{\prime }(a)\mathrm{\Delta }x+ϵ\mathrm{\Delta }x& & (\mathrm{\Delta }x\to 0일때ϵ\to 0)\end{array}$$
그리고 이렇게 표현함으로써 ${\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}$ 처럼 $\mathrm{\Delta }x$ 가 분모에 들어가는 일을 방지할 수 있다.

참고로 이 표현법이 나중에 다변수함수의 미분가능성, 연쇄법칙 얘기할 때 또 나오므로 잘 기억해두자.

 

${\displaystyle \frac{dy}{dx}}$ 가 미분계수라면 $ϵ$ 은 선형근사와 실제 값 사이의 오차계수(?) 쯤으로 생각할 수 있다. 그림에서 $\mathrm{\Delta }x\to 0$ 일 때 $ϵ$ (실제와 선형근사의 차이나는 정도의 비율) 이 어떤 값으로 수렴할지 생각해보자

연쇄 법칙의 증명

---

$u=g(x)$ 가 $x=a$ 에서 미분 가능하고 $g(a)=b$ 이며
$y=f(u)$ 가 $u=b$ 에서 미분 가능하다고 하자.

그러면 바로 위에서 언급한 $(식1)$ 에 의해 $\mathrm{\Delta }u$ 는 다음과 같이 표현된다

$$\begin{array}{}\text{(식 2)}& \mathrm{\Delta }u=g^{\prime }(a)\mathrm{\Delta }x+{ϵ}_1\mathrm{\Delta }x=[g^{\prime }(a)+{ϵ}_1]\mathrm{\Delta }x\end{array}$$

여기서 $\mathrm{\Delta }x\to 0$ 일 때 ${ϵ}_1\to 0$ 이다.

같은 방법으로 $\mathrm{\Delta }y$ 는 다음과 같이 표현된다.
$$\begin{array}{}\text{(식 3)}& \mathrm{\Delta }y=f^{\prime }(b)\mathrm{\Delta }u+{ϵ}_2\mathrm{\Delta }u=[f^{\prime }(b)+{ϵ}_2]\mathrm{\Delta }u\end{array}$$

여기서 $\mathrm{\Delta }u\to 0$ 일 때 ${ϵ}_2\to 0$ 이다.

 

$(식3)$ 의 $\mathrm{\Delta }u$ 자리에 $(식2)$ 를 대입하면 다음을 얻는다.

$$\mathrm{\Delta }y=[f^{\prime }(b)+{ϵ}_2][g^{\prime }(a)+{ϵ}_1]\mathrm{\Delta }x$$

 

양변을 $\mathrm{\Delta }x$로 나누면 ($\mathrm{\Delta }x\ne 0$ 이므로 가능하다.)

$${\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}=[f^{\prime }(b)+{ϵ}_2][g^{\prime }(a)+{ϵ}_1]$$

 

여기서 $\mathrm{\Delta }x\to 0$ 이면 $(식2)$ 에 의해 $\mathrm{\Delta }u\to 0$ 이다.
따라서 $\mathrm{\Delta }x\to 0$ 이면 ${ϵ}_1\to 0$ 이고 ${ϵ}_2\to 0$ 이게 되며 다음이 성립하게 된다.
$$\begin{array}{rl}{\displaystyle \frac{dy}{dx}}=\underset{\mathrm{\Delta }x\to 0}{lim}{\displaystyle \frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}}=& \underset{\mathrm{\Delta }x\to 0}{lim}[f^{\prime }(b)+{ϵ}_2][g^{\prime }(a)+{ϵ}_1]\\ =& f^{\prime }(b)g^{\prime }(a)\\ =& f^{\prime }(g(a))g^{\prime }(a)\end{array}$$

 

이것으로 연쇄법칙이 증명되었다.

---

예제

$(Q1)$ $f(x)=x\sqrt{2-x^2}$ 일 때 $f^{\prime }(x)$ 를 구하라.

풀이

$g(x)=\sqrt{2-x^2}$ 라 하면 $f(x)=xg(x)$ 이다.

곱의 미분을 적용하면 
$$\begin{array}{}\text{(1)}& f^{\prime }(x)=g(x)+x{g}^{\prime }(x)\end{array}$$

한편 $g(x)$는 
$h(u)=\sqrt{u}$, $u(x)=2-x^2$ 의 합성함수인 $(h\circ u)(x)$ 라고 볼 수 있다.

따라서 연쇄법칙을 적용하면 

$$\begin{array}{rl}{g}^{\prime }(x)=& {\displaystyle \frac{dh}{du}}\cdot {\displaystyle \frac{du}{dx}}\\ =& {\displaystyle \frac{1}{2\sqrt{u}}}\cdot (-2x)\\ =& {\displaystyle \frac{1}{2\sqrt{2-x^2}}}\cdot (-2x)\\ =& {\displaystyle \frac{-x}{\sqrt{2-x^2}}}\end{array}$$

이것을 $(1)$ 에 대입하면 최종적으로 다음을 얻는다.
$$f^{\prime }(x)=\sqrt{2-x^2}-{\displaystyle \frac{x^2}{\sqrt{2-x^2}}}$$

---

$(Q2)$ $f(x)=3x^2+2$ 에 대하여 본문에서 언급한
$\mathrm{\Delta }y=f^{\prime }(x)\mathrm{\Delta }x+ϵ\mathrm{\Delta }x$ 꼴을 만들었을 때
$\mathrm{\Delta }x$ 에 대한 함수 $ϵ$ 를 구하라

 

풀이

$\mathrm{\Delta }y$ 의 정의에 따라 다음이 성립한다.

$$\begin{array}{rl}\mathrm{\Delta }y=& f(x+\mathrm{\Delta }x)-f(x)\\ =& [3(x+\mathrm{\Delta }x{)}^2+2]-[3x^2-2]\\ =& [3x^2+6x(\mathrm{\Delta }x)+3(\mathrm{\Delta }x{)}^2+2]-[3x^2+2]\\ =& 6x(\mathrm{\Delta }x)+3(\mathrm{\Delta }x{)}^2\end{array}$$

한편 $f^{\prime }(x)=6x$ 이므로 
위에서 구한 $\mathrm{\Delta }y=6x(\mathrm{\Delta }x)+3(\mathrm{\Delta }x{)}^2$ 와 
$\mathrm{\Delta }y=f^{\prime }(x)\mathrm{\Delta }x+ϵ\mathrm{\Delta }x$ 를 비교하면 $ϵ=3\mathrm{\Delta }x$ 임을 알 수 있다.

+ ($ϵ$ 이 $\mathrm{\Delta }x$ 에 대한 함수라고 한 점에 대해 생각해보자.)

 

 

 

이전글 : 7. 미분 공식 (Differentiation Formulas)

다음글 : 9. 음함수의 미분법 (Implicit Differentiation)