1. 함수의 극한 (Limits of functions)
2. 극한의 엄밀한 정의, 엡실론 델타 논법(Epsilon-delta argument)
3. 극한법칙과 압축정리 (Limit laws and Squeeze Theorem)
4. 함수의 연속과 중간값 정리 (Continuity and Intermediate Value Theorem)
와 관련된 연습문제들을 모아놓은 포스트이다.
가급적 위 포스트들을 모두 공부한 후 풀어보기를 권장한다.
쉽게 풀이를 찾을 수 있는 기본 연습문제는 조금만 싣고 생각을 조금 해보아야 하는 문제들을 담았다.
초반 문제들은 부연설명을 자세하게 달았지만 뒤로 갈수록 핵심적인 내용 외의 설명은 생략했으므로
만약 이런 문제들을 처음 접한다면 초반 문제부터 순서대로 푸는것이 좋다.
(다만 난이도가 꼭 오름차순 배치인것은 아니다)
문제들이 계속 추가될 수도 있다.
1. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오
$$ \lim_{x \to 3} 3x - 2 = 7 $$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x-3| < \delta \Longrightarrow |(3x-2) - 7| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( |(3x-2) - 7| = |3x - 9| = 3|x-3| < 3\times \delta \) 이므로
\(3\delta = \epsilon\), 즉 \( \delta = \dfrac{\epsilon}{3} \)으로 설정하면
\( 0 < |x-3| < \delta \Longrightarrow |(3x-2) - 7| = 3|x-3| < 3 \times \delta = 3 \times \dfrac{\epsilon}{3} = \epsilon \) 이다.
따라서 극한의 정의에 의해 \(\lim\limits_{x \to 3} 3x - 2 = 7\)이다.
2. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (스튜어트 예제, 연세대학교 편입 2010 기출)
$$ \lim_{x \to 0} \dfrac{1}{x^{2}} = \infty $$
풀이
임의의 큰 수 \(M > 0\) 에 대해
\( 0< |x-0| < \) \(\delta\) 이면 \(\dfrac{1}{x^{2}} > M \) 을 만족하게 하는 \(\delta > 0 \) 이 존재하는지 살펴보아야 한다.
그리고 다음이 성립한다.
\( \begin{align} \dfrac{1}{x^{2}} > M &\Longleftrightarrow x^{2} < \dfrac{1}{M} \\ &\Longleftrightarrow \sqrt{x^{2}} < \sqrt{\dfrac{1}{M}} \\ &\Longleftrightarrow |x| < \dfrac{1}{\sqrt{M}} \end{align} \)
참고로 여기서 양방향 화살표를 이용했다. 즉 화살표 좌우가 필요충분조건으로 언제든지 넘나들 수 있는 논리라는 얘기다.
이제 \( \delta = \dfrac{1}{\sqrt{M}} \) 라고 한다면 \(0 < |x| < \dfrac{1}{\sqrt{M}} \)이고
위의 양방향 화살표를 타고 올라가면 원하는 부등식인 \(\dfrac{1}{x^{2}} > M \) 를 얻는다.
정리하자면, \( \delta = \dfrac{1}{\sqrt{M}} \) 으로 설정하면
\( 0< |x-0| < \) \(\delta\) 일 때 \(\dfrac{1}{x^{2}} > M \) 을 만족하므로
무한극한의 정의에 의해 \( \lim\limits_{x \to 0} \dfrac{1}{x^{2}} = \infty \) 이다.
3. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오
$$ \lim_{x \to 2} x^{2} = 4 $$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x-2| < \delta \Longrightarrow |x^{2} - 4| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( |x^{2} - 4| = |(x+2)(x-2)| = |x+2||x-2| \)이고,
\(|x-2|\)는 \(\delta\)보다 작으므로 \( |x+2| \) 가 어떠한 값보다 작게 만드는 방법을 찾아야 한다.
우리는 \(x=2\) 근처의 값에 관심이 있다. 따라서 \(\delta = 1\)로 설정하여
\(x\)와 \(2\)의 거리인 \( |x-2| \) 를 1보다 작게 제한시켜놓고 살펴보자.
\( \delta = 1 \) 이면 ( = \(x\)와 \(2\)의 거리를 1 미만으로 설정하면)
\( 0 < |x-2| < 1 \Longrightarrow 1<x<3, x \neq 2 \) 를 얻고
각 항에 \(2\)를 더하면 $ 3 < x+2 < 5, x + 2 \neq 4 $ 즉 $ |x+2| < 5 $를 얻는다.
또 한 편 \(\delta = \dfrac{\epsilon}{5} \) 으로 설정하면 ( = \(x\)와 \(2\)의 거리를 \(\dfrac{\epsilon}{5}\) 미만으로 설정하면)
\(0 < |x-2| < \delta = \dfrac{\epsilon}{5} \) 이므로 \(|x-2| < \dfrac{\epsilon}{5}\) 을 얻는다.
이제 \(\delta = \text{min(}1, \dfrac{\epsilon}{5} \text{)} \) 라고 하면
\(|x+2| < 5\) 와 \(|x-2| < \dfrac{\epsilon}{5}\)를 동시에 만족하므로
\( 0 < |x-2| < \delta \Longrightarrow |x^{2} - 4| = |x+2||x-2| < 5 \times \dfrac{\epsilon}{5} = \epsilon \) 이다.
따라서 극한의 정의에 의해 \(\lim\limits_{x \to 2} x^{2} = 4\) 이다.
4. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (고려대학교 편입 비수학과 2018 & 연세대학교 편입 2007 기출문제)
$$ \lim_{x \to 0} \dfrac{x+1}{x^{2} + 1} = 1 $$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x| < \delta \Longrightarrow \left|\dfrac{x+1}{x^{2} + 1} - 1\right| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( \left|\dfrac{x+1}{x^{2} + 1} - 1\right| = \left|\dfrac{x-x^{2}}{x^{2} + 1}\right| = \dfrac{|x-1|}{|x^{2}+1|}|x| \) 이고
\(\delta = 2\) 라고 하면 \(0 < |x| < 2 \Longrightarrow -2 < x < 2, x \neq 0\) 이고 각 항에 \(-1\)을 더하면
\( -3< x-1 < 1, x \neq 1 \)을 얻는다.
따라서 \(\delta = 2\) 일 때 \(|x-1| < 3\) 이다. (왜 $1$이 아닌지는 직접 대입해보라.)
또 역시 \(\delta = 2\)에서는 \( 0 < |x| < 2 \) 이므로
\( 0< x^{2} < 4 \Longrightarrow 1< |x^{2}+1| < 5\) 이고 \( \dfrac{1}{5}<\dfrac{1}{|x^2 + 1|} < 1 \) 을 얻는다.
그리고 \( \delta = \dfrac{\epsilon}{3} \) 이라 하면 \( |x| < \dfrac{\epsilon}{3} \)을 얻으므로
\(\delta = \text{min(}2, \dfrac{\epsilon}{3} \text{)} \) 이라고 설정하면
\(|x-1| < 3\), \( \dfrac{1}{|x^2 + 1|} < 1 \), \( |x| < \dfrac{\epsilon}{3} \) 을 모두 만족시키므로
\( 0 < |x| < \delta \Longrightarrow \left|\dfrac{x+1}{x^{2} + 1} - 1\right| = \\ \dfrac{|x-1|}{|x^{2}+1|}|x| < 3 \times 1 \times \dfrac{\epsilon}{3} = \epsilon\) 이다.
따라서 극한의 정의에 의해 \( \lim\limits_{x \to 0} \dfrac{x+1}{x^{2} + 1} = 1 \) 이다.
5. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (연세대학교 편입 2012 기출문제)
$$ \lim_{x \to 2} \dfrac{1}{ \sqrt{x} + \sqrt{2} } = \dfrac{1}{2\sqrt{2}}$$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x-2| < \delta \Longrightarrow \left| \dfrac{1}{ \sqrt{x} + \sqrt{2} } - \dfrac{1}{2\sqrt{2}} \right| < \epsilon \)을 만족하는지 살펴보아야 한다.
한편 다음이 성립하고
\( \left| \dfrac{1}{ \sqrt{x} + \sqrt{2} } - \dfrac{1}{2\sqrt{2}} \right| = \left| \dfrac{ \sqrt{2} - \sqrt{x} }{ 2\sqrt{2} (\sqrt{x} + \sqrt{2} ) } \right| = \dfrac{|x-2|}{2\sqrt{2}(\sqrt{x} + \sqrt{2})^{2}} \)
\(|x-2|\)는 \(\epsilon\) 을 포함한 식으로 원하는 값보다 작게 쉽게 만들 수 있으므로
\( \dfrac{1}{(\sqrt{x} + \sqrt{2})^{2} } \) 를 어떤 값보다 작게 만들어보자.
\(|x-2| < a\)로 범위를 제한했다 치면
\( \begin{align} 2-a<x \Longrightarrow &\sqrt{2-a} < \sqrt{x} \\ \Longrightarrow &\sqrt{2-a} + \sqrt{2} < \sqrt{x} + \sqrt{2} \end{align} \)
계산을 간편하게 하기 위해 \(\sqrt{2-a}\) 를 \(k\sqrt{2}\), (\( k \in \mathbb{R} \)) 꼴로 만들어보자
\(a = \dfrac{3}{2}\) 이면 \(\sqrt{2-a} = \sqrt{\dfrac{1}{2}} = \dfrac{\sqrt{2}}{2}\) 이므로 \( \sqrt{2} + \sqrt{2-a} = \dfrac{3}{2}\sqrt{2} \) 이다.
따라서 \(a = \dfrac{3}{2} \) 이면
\( \begin{align} \dfrac{3}{2}\sqrt{2} < \sqrt{x} + \sqrt{2} \Longrightarrow &\dfrac{9}{2} < (\sqrt{x} + \sqrt{2})^{2} \\ \Longrightarrow &\dfrac{1}{ (\sqrt{x} + \sqrt{2})^{2} } < \dfrac{2}{9} \end{align} \)
아까 위에서 \(|x-2|\)는 원하는 값보다 쉽게 작게 만들 수 있다고 하였다.
그리고 위에서 \(|x-2| < a = \dfrac{3}{2} \) 인 상황에서는 \( \dfrac{1}{ ( \sqrt{x} + \sqrt{2} )^{2} } < \dfrac{2}{9} \)라고 하였으므로
이 원하는 값을 \(\epsilon \times 2\sqrt{2} \times \dfrac{9}{2} = 9\sqrt{2}\epsilon \) 으로 설정하면
\(|x-2| < \dfrac{3}{2} \), \( |x-2| <9\sqrt{2}\epsilon \) 을 동시에 만족하는 상황에서
\( \dfrac{|x-2|}{2\sqrt{2}(\sqrt{x} + \sqrt{2})^{2}} < \dfrac{1}{2\sqrt{2}} \times \dfrac{2}{9} \times 9\sqrt{2}\epsilon = \epsilon \) 을 만족하여 원하는 꼴이 유도될 것이다.
따라서 \(\delta = \text{min(}\dfrac{3}{2}, 9\sqrt{2}\epsilon \text{)} \) 라고 하면
\( 0 < |x-2| < \delta \) 일 때 \( \left| \dfrac{1}{ \sqrt{x} + \sqrt{2} } - \dfrac{1}{2\sqrt{2}} \right| = \dfrac{|x-2|}{2\sqrt{2}(\sqrt{x} + \sqrt{2})^{2}} < \epsilon \) 을 만족하므로
극한의 정의에 의해 \( \lim\limits_{x \to 2} \dfrac{1}{ \sqrt{x} + \sqrt{2} } = \dfrac{1}{2\sqrt{2}} \)이다.
6. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (연세대학교 편입 2006 기출문제)
$$ \lim_{x \to 0} x \cos{\left( \dfrac{1}{x} \right)} = 0 $$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x| < \delta \Longrightarrow \left| x \cos{ \left( \dfrac{1}{x} \right) } \right| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( \left| x \cos{ \left( \dfrac{1}{x} \right) } \right| = |x| \left| \cos{\left( \dfrac{1}{x} \right)} \right| \) 이고
모든 \(x\) 에 대해 \( \cos{ \left( \dfrac{1}{x} \right) } \le 1\) 이므로
\(\delta = \epsilon\) 이라고 하면
\( 0 < |x| < \delta \Longrightarrow \left| x \cos{ \left( \dfrac{1}{x} \right) } \right| = |x| \left| \cos{ \left( \dfrac{1}{x} \right) } \right| < 1 \times \epsilon = \epsilon \) 이다.
따라서 극한의 정의에 의해 \( \lim\limits_{x \to 0} x \cos{ \left( \dfrac{1}{x} \right) } = 0 \)
7. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (고려대학교 편입 수학과 2018 기출문제)
$$ \lim_{x \to 0} (1 + \text{sin}x)^{2} = 1 $$
풀이
먼저 \( |x| < \dfrac{\pi}{2} \) 이면 \( |\text{sin} x| \le |x| \) 임을 증명하자.
\(x = 0\) 이면 \(0 \le 0\) 이므로 성립한다.
\(0 < x < \dfrac{\pi}{2} \) 인 경우
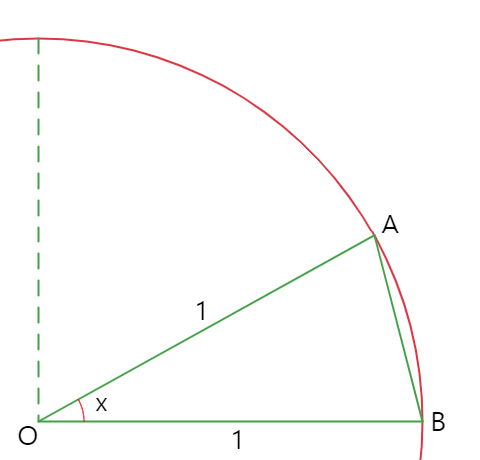
왼쪽 그림은 점 \(O\)를 중심으로 반지름이 1인 원에
원 위의 두 점 \(A, B\)와 점 \(O\)를 꼭짓점으로 하는 삼각형이다.
삼각형의 넓이는 \(1 \times 1\text{sin}x \times \dfrac{1}{2} = \dfrac{\text{sin}x}{2}\) 이고
부채꼴 \(OAB\)의 넓이는 \( \dfrac{1}{2} \times 1^{2} \times x = \dfrac{x}{2} \) 이다.
부채꼴의 넓이가 삼각형보다 더 크거나 같으므로
\(\dfrac{\text{sin}x}{2} \le \dfrac{x}{2} \Longrightarrow \text{sin}x \le x \)
\(-\dfrac{\pi}{2} < x < 0 \) 인 경우
\(-x = t\) 라고 하면 \(0 < t < \dfrac{\pi}{2} \) 이고
이 범위에서는 \(\text{sin}t \le t \) 임을 위에서 보였다.
따라서 \( \text{sin}t \le t \) 의 \(t\)에 \(-x\)를 대입하면 \( \text{sin}(-x) \le -x \) \(\Longrightarrow \) \( -\text{sin}x \le -x \)
따라서 \( |x| < \dfrac{\pi}{2} \) 이면 \( |\text{sin}x| < |x| \) 이다.
이제 본론으로 돌아오자.
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x| < \delta \Longrightarrow |(1 + \text{sin}x)^{2} -1| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( |(1 + \text{sin}x)^{2} -1| = |\text{sin}x||\text{sin}x + 2| \)
\(|x| < \dfrac{\pi}{2} \) 이면 \( |\text{sin}x| < |x| \)임은 위에서 보였고
여기서 \(|x| < \dfrac{\epsilon}{3} \)을 추가로 만족한다면
\( |\text{sin}x| < |x| < \dfrac{\epsilon}{3}\) 를 만족한다.
그리고 \(|\text{sin}x + 2| \le 3\)이므로 \(\delta = \text{min(}\dfrac{\pi}{2}, \dfrac{\epsilon}{3} \text{)} \) 라고 하면
\( 0 < |x| < \delta \Longrightarrow |(1 + \text{sin}x)^{2} -1| = |\text{sin}x||\text{sin}x + 2| < \dfrac{\epsilon}{3} \cdot 3 = \epsilon \)
이므로 극한의 정의에 의해 \( \lim\limits_{x \to 0} (1 + \text{sin}x)^{2} = 1 \)
8. 다음을 \( \epsilon-\delta \) 논법으로 증명하시오 (연세대학교 편입 2009 기출문제)
$$ \lim_{x \to 2} \left(x^{3} - 3x + 1\right) = 3 $$
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x-2| < \delta \Longrightarrow \left| x^{3} - 3x + 1 - 3 \right| < \epsilon \)을 만족하는지 살펴보아야 한다.
\( \left| x^{3} - 3x + 1 - 3 \right| = (x+1)^{2}|x-2| \) 이고
\(\delta = 1\) 이라 하면 \( 0 < |x-2| < 1 \Longrightarrow 2<x+1<4, x \neq 3 \) 이므로
\(|x+1|<4 \Longrightarrow (x+1)^{2} < 16 \) 를 얻는다.
따라서 \(\delta = \text{min(}1, \dfrac{\epsilon}{16} \text{)} \) 이라고 하면
\( 0 < |x-2| < \delta \Longrightarrow \left| x^{3} - 3x + 1 - 3 \right| = (x+1)^{2}|x-2| < 16 \cdot \dfrac{\epsilon}{16} = \epsilon \) 이다.
따라서 극한의 정의에 의해 \(\lim\limits_{x \to 2} \left(x^{3} - 3x + 1\right) = 3\) 이다.
9. 함수 \(f\) 가 \(x=3\)에서 연속인지 불연속인지 \(\epsilon - \delta\) 논법을 사용하여 증명하시오.
(단 \( \mathbb{Q} \)는 유리수 전체의 집합이다.) (연세대학교 편입 2015 기출문제)
$$ f(x) = \begin{cases} \begin{align} x^{2}& &(x \in \mathbb{Q}) \\ 3x& &(x \notin \mathbb{Q}) \end{align} \end{cases}$$
풀이
연속의 정의에 의해 \(\lim\limits_{x \to 3} f(x) = f(3) = 9\) 임을 증명하면 \(x=3\) 에서 연속임이 증명된다.
\(x \in \mathbb{Q}\) 일 때 \(f(x) = x^{2}\) 이고 \(x \notin \mathbb{Q}\) 일 때 \(f(x) = 3x\) 이므로
임의의 \(\epsilon > 0\)에 대해 \(\delta_{1}, \delta_{2} > 0\)이 존재하여
$$ \begin{align} & 0 < |x-3| < \delta_{1} \Longrightarrow |x^{2} - 9| < \epsilon \\ & 0<|x-3|<\delta_{2} \Longrightarrow |3x - 9| < \epsilon \end{align} $$
을 만족함을 보이자.
\(x \in \mathbb{Q}\) 인 경우
\(|x^{2}-9| =|x+3||x-3| \) 이고 \(0 < |x-3| < 1 \) 로 제한하면
\(0 < |x-3| < 1 \Longrightarrow -1< x-3 < 1, x \neq 3 \Longrightarrow 5 < x+3 < 7, x \neq 6 \)
따라서 \( |x+3| < 7 \) 를 얻는다.
즉 \( 0 < |x-3| < 1 \) 이면 \(|x+3| < 7\)이다.
또 \( 0 < |x-3| < \dfrac{\epsilon}{7} \) 으로 제한하면
\( 0 < |x-3| < \dfrac{\epsilon}{7} \)일 때 \( |x-3| < \dfrac{\epsilon}{7} \) 이므로
\(\delta_{1} = \text{min(}1, \dfrac{\epsilon}{7} \text{)} \) 으로 설정하면
\(0 < |x-3| < \delta_{1} \Longrightarrow |x^{2} - 9| = |x+3||x-3| < 7 \cdot \dfrac{\epsilon}{7} = \epsilon \)
\(\delta_{1} > 0\)의 존재성을 보였으므로 \(x \in \mathbb{Q} \) 에 대해서는 극한이 존재한다.
\(x \notin \mathbb{Q}\) 인 경우
\(|3x - 9| = 3|x-3|\) 이므로 \(\delta_{2} = \dfrac{\epsilon}{3} \) 으로 설정하면
\( 0 < |x-3| < \delta_{2} \Longrightarrow |3x-9| = 3|x-3| < 3 \cdot \dfrac{\epsilon}{3} = \epsilon \)
\(\delta_{2} > 0\)의 존재성을 보였으므로 \(x \notin \mathbb{Q} \) 에 대해서도 극한이 존재한다.
이제 \( \delta = \text{min(}\delta_{1}, \delta_{2}\text{)} \) 라고 하면
\(x \in \mathbb{R} \) 에서 \(0 < |x-3| < \delta \Longrightarrow |f(x) - 9| < \epsilon\) 가 성립하므로
극한의 정의에 의해 \(\lim\limits_{x \to 3} f(x) = 9\) 이다. 따라서 \(f(x)\) 는 \(x=3\) 에서 연속이다.
10. 함수 \(f\)가 다음과 같을 때 어떤 점에서 연속인지 설명하시오. (스튜어트 연습문제, 연세대학교 편입 2010 기출)
$$ f(x) = \begin{cases} \begin{align} 0 &&(x \in \mathbb{Q}) \\ 1 &&(x \notin \mathbb{Q}) \end{align} \end{cases}$$
풀이
\(f(x)\) 가 임의의 점 \(x = a\)에서 연속이려면
\(\lim\limits_{x \to a} f(x) = f(a) \) 를 만족해야 한다.
연속의 조건 중 "극한이 존재한다"가 모순임을 보임으로써 연속이 아님을 증명할 것이다.
\(\lim\limits_{x \to a} f(x) \) 가 \(L\)로 존재한다고 가정하여 모순을 이끌어내자 (귀류법)
\( \lim\limits_{x \to a} f(x) = L \) 이므로 임의의 \(\epsilon > 0\)에 대해 \(\delta_{1}, \delta_{2} > 0\)가 존재하여
\(( x \in \mathbb{Q}) \) 에서 \(0 < |x-a| < \delta_{1} \Longrightarrow |f(x)-f(a)| < \epsilon \) 을 만족하고
\( (x \notin \mathbb{Q}) \) 에서 \(0 < |x-a| < \delta_{2} \Longrightarrow |f(x) - f(a)| < \epsilon \) 을 만족하여야 한다.
임의의 \(\epsilon > 0\)에 대해서 만족하여야 하는데, \(\epsilon = \dfrac{1}{4} \) 라고 설정해보면
\( (x \in \mathbb{Q}) \) 인 경우 \(f(x) = 0\) 이므로
\(0 < |x-a| < \delta_{1} \Longrightarrow |0-f(a)| < \dfrac{1}{4} \Longrightarrow -\dfrac{1}{4} < f(a) < \dfrac{1}{4} \) 이고
\( (x \notin \mathbb{Q}) \) 인 경우 \(f(x) = 1\) 이므로
\(0 < |x-a| < \delta_{1} \Longrightarrow |1-f(a)| < \dfrac{1}{4} \Longrightarrow \dfrac{3}{4} < f(a) < \dfrac{5}{4} \) 인데
이를 동시에 만족하는 \(f(a)\) 는 존재할 수 없다.
따라서 가정인 \( \lim\limits_{x \to a} f(x) = f(a) \) 는 모순이고 극한이 존재하지 않는다.
모든 점에서 극한이 존재하지 않으므로 모든 점에서 연속이 아니다.
11. 함수 \(f : \mathbb{R} \rightarrow \mathbb{R}\) 가 \(\lim\limits_{x \to 0} f(x) = 1 \)을 만족한다고 하자.
그러면 \(\lim\limits_{x \to 0} (f(x))^{2} = 1 \) 을 만족함을 \(\epsilon - \delta\) 논법으로 증명하시오 (연세대학교 편입 2021 기출문제)
풀이
임의의 \(\epsilon > 0\) 에 대해 \( \delta > 0 \)이 존재하여
\( 0 < |x| < \delta \Longrightarrow \left| (f(x))^{2} - 1 \right| < \epsilon \)을 만족하는지 살펴보아야 한다.
우선 다음을 관찰하자.
\( \left| (f(x))^{2} - 1 \right| = |f(x) + 1||f(x) - 1| \)
\( |f(x)+1| \) 와 \( |f(x) - 1| \) 이 모두 무언가보다 작게 만들어야 한다.
후자는 \(\lim\limits_{x \to 0} f(x) = 1 \) 가 주어져 있으므로 쉽게 무언가 보다 작게 만들 수 있다.
전자에 대해 구해보자.
\(\lim\limits_{x \to 0} f(x) = 1 \) 가 주어져 있다.
따라서 \(\delta_{1} > 0 \) 이 존재하여 \(0 < |x| < \delta_{1} \Longrightarrow |f(x) - 1| < 1 \) 을 만족한다.
그리고 삼각부등식에 의해 이러한 \(x\) 에서는 \(|f(x) + 1| = |(f(x) - 1) + 2| < |f(x) - 1| + |2| < 3\) 을 만족한다.
즉, \(0 < |x| < \delta_{1} \) 에서는 \(|f(x) + 1| < 3 \) 이다.
또 \(\delta_{2} > 0\) 역시 존재하여 \(0 < |x| < \delta_{2} \Longrightarrow |f(x) - 1| < \dfrac{\epsilon}{3} \) 을 만족하므로
\(\delta = \text{min(}\delta_{1}, \delta_{2}\text{)}\) 으로 설정하면
\( 0 < |x| < \delta \Longrightarrow \left| (f(x))^{2} - 1 \right| = |f(x) + 1||f(x) - 1| < 3\times\dfrac{\epsilon}{3} = \epsilon \) 이므로
극한의 정의에 의해 \(\lim\limits_{x \to 0} (f(x))^{2} = 1 \) 이다.
12. 함수 \(f \) 가 다음과 같이 정의되어 있다.
$$ f(x) = \begin{cases} \begin{align} &\text{sin}x &(x \in \mathbb{Q}) \\ &x(x+1) &(x \notin \mathbb{Q}) \end{align} \end{cases} $$
\(\lim\limits_{x \to 0} \dfrac{\text{sin}x}{x} = 1 \) 임을 이용하여 \(f\) 가 \(x=0\) 에서 미분가능함을 \(\epsilon - \delta \) 논법으로 증명하시오. (\(\mathbb{Q}\) 는 유리수 전체의 집합) (연세대학교 편입 2020 기출)
(이 문제는 미분가능성에 대해 먼저 공부한 사람만 풀면 된다.)
풀이
\(x=0\) 에서 미분 가능하려면 미분계수의 정의에 따라 다음의 극한이 존재하면 된다.
$$ \lim_{x \to 0} \dfrac{f(x) - f(0)}{x - 0} $$
\(0 \in \mathbb{Q} \) 이므로 \(f(0) = 0 \) 이고 따라서 다음의 극한이 존재함을 보이면 된다.
$$ \lim_{x \to 0} \dfrac{f(x)}{x} $$
\((x \in \mathbb{Q})\) 일 때는 \(\dfrac{f(x)}{x} = \dfrac{\text{sin}x}{x} \) 이고
\(\lim\limits_{x \to 0} \dfrac{\text{sin}x}{x} = 1 \) 가 주어져 있으므로
\( \delta_{1} > 0 \) 이 존재하여
\(0 < |x| < \delta_{1} \Longrightarrow \left|\dfrac{\text{sin}x}{x} - 1 \right| < \epsilon \) 을 만족한다.
\((x \notin \mathbb{Q})\) 일 때는 \(\dfrac{f(x)}{x} = \dfrac{x(x+1)}{x} = x+1\) 이므로
\(\delta_{2} > 0 \) 가 존재하여 \(0 < |x| < \delta_{2} \Longrightarrow |x+1 - 1| < \epsilon \) 을 만족하는지 살펴보아야 한다.
\( |x+1 - 1| = |x| \) 이므로 \(\delta_{2} = \epsilon\) 이라고 하면
\(0 < |x| < \delta_{2} \Longrightarrow |x+1 - 1| = |x| < \delta = \epsilon \) 이므로 만족한다.
따라서 \(\delta = \text{min(}\delta_{1}, \delta_{2}\text{)}\) 으로 설정하면
\(0 < |x| < \delta_{1}\), \(0 < |x| < \delta_{2}\) 가 동시에 만족하므로
\((x \in \mathbb{Q})\) 일 때와 \((x \notin \mathbb{Q})\) 일 때 모두 \( \left| \dfrac{f(x)}{x} - 1 \right| < \epsilon \) 이 만족하게 되고
따라서 \(( x \in \mathbb{R} )\) 일 때 \(0 < |x| < \delta \Longrightarrow \left| \dfrac{f(x)}{x} - 1 \right| < \epsilon \) 이 만족한다.
따라서 극한의 정의에 의해 \( \lim\limits_{x \to 0} \dfrac{f(x)}{x} = 1 \) 이고 \(f(x)\) 는 \(x=0\) 에서 미분가능하다.
13. \(f(x) = x^{2} + 10\text{sin}x\) 이면 \(f(c) = 1000 \) 을 만족하는 \(c\) 가 존재함을 보여라.
(스튜어트 연습문제)
풀이
\(f(x)\) 는 다항함수와 삼각함수의 합이므로 각각이 정의되는 정의역의 교집합에서 연속이다.
따라서 실수 전체에서 연속이다.
\( f(a) < 1000 \) 인 \( a \) 를 찾고
\( f(b) > 1000 \) 인 \( b \) 를 찾아 중간값 정리를 이용하여
\( f(c) = 1000 \) 인 \(c \in (a, b)\) 가 존재함을 증명할 것이다.
\(-10 \le 10 \text{sin}x \le 10 \) 이므로
\(x = \sqrt{900}\) 이라 하면 \(f(x) = 900 + 10\text{sin}x \le 910 \) 이다.
또 \(x = \sqrt{1100}\) 이라 하면 \(f(x) = 1100 + 10\text{sin}x \geq 1090 \) 이다.
따라서 중간값 정리에 의해 \( f(c) = 1000 \) 이 되는 \(c \in (\sqrt{900}, \sqrt{1100})\) 이 존재한다.
14. \(\text{cos}x = x^{3}\) 에 대해 방정식이 적어도 하나의 실근을 가짐을 증명하라. (스튜어트 연습문제)
풀이
\(f(x) = \text{cos}x - x^{3}\) 라고 하자.
삼각함수와 다항식의 차이므로 \(f(x)\)는 실수 전체에서 연속이다.
그리고
\(f(0) = 1 > 0\),
\(f(\pi) = -1 - \pi^{3} < 0\) 이므로
중간값 정리에 의해 \(f(c) = 0 \) 을 만족하는 \(c \in (0, \pi) \) 가 존재한다.
이는 방정식의 근이므로 \(\text{cos}x = x^{3}\) 는 적어도 하나의 실근을 갖는다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 6. 도함수와 미분가능성 (Derivative and Differentiability) (4) | 2021.01.11 |
|---|---|
| 5. 함수의 기울기와 미분계수 (Slope and Derivative of a function) (0) | 2021.01.06 |
| 4. 함수의 연속과 중간값 정리 (Continuity and Intermediate Value Theorem) (0) | 2021.01.03 |
| 3. 극한법칙과 압축정리 (Limit laws and Squeeze Theorem) (2) | 2021.01.02 |
| 2. 극한의 엄밀한 정의, 엡실론 델타 논법(Epsilon-delta argument) (2) | 2021.01.02 |