*모바일에서는 일부 수식이 잘려 안보일 수 있습니다
이전 포스팅에서는 간단한 함수에 대해 엄밀한 정의를 통해 극한을 계산하였다.
이제는 극한법칙을 이용해 복잡한 다항식이나 유리식의 극한을 계산하는 법을 알아볼 차례이다.
다음과 같은 극한 법칙이 알려져 있다.
\(c\)가 실수이고 \( \lim\limits_{x \to a} f(x) = L\), \( \lim\limits_{x \to a} g(x) = M \)으로 모두 수렴한다면
$$ \begin{align} \lim_{x \to a} [f(x) \pm g(x)] =& &L \pm M& \\ \lim_{x \to a} cf(x) =& &cL& \\ \lim_{x \to a} f(x)g(x) =& &LM& \\ \lim_{x \to a} \dfrac{f(x)}{g(x)} =& &\dfrac{L}{M}& \text{ (only when } M \neq 0 \text{ )} \end{align} $$
아래의 증명이 복잡해 보이더라도 색과 띄어쓰기로 가독성을 높이고, 부연설명을 상세하게 넣어서 이해를 돕도록 했으므로 꼭 한 번 읽고 손으로 직접 작성해보기를 강력히 추천한다.
이후에 풀 연습문제의 이해에도 큰 도움이 된다.
\( 1. \) \( \lim\limits_{x \to a} [f(x) + g(x)] = L + M \) 증명
임의의 \(\epsilon > 0\)에 대해 \( 0 < |x-a| < \delta \) \( \Longrightarrow \) \(|f(x) + g(x) - (L + M)| < \epsilon\)
을 만족하는 \( \delta > 0\)이 존재하는지 찾아야 한다.
삼각부등식을 이용하면 다음과 같다.
\( \begin{align} |f(x) + g(x) - (L + M)| &=& |(f(x) - L) + (g(x) - M)| \\ &\textcolor{red}{\le}& |f(x) - L| + |g(x)-M| \tag{1} \end{align} \)
한편, 가정에 의해 \(\lim\limits_{x \to a} f(x) = L\), \(\lim\limits_{x \to a} g(x) = M\)으로 수렴하므로
극한의 정의에 의해 다음을 만족하는 \(\delta_{1}, \delta_{2}\)가 존재한다.
\( 0< |x-a| < \delta_{1}\) 일 때 \(|f(x) - L| < \frac{\epsilon}{2} \)
\( 0< |x-a| < \delta_{2}\) 일 때 \(|g(x) - M| < \frac{\epsilon}{2} \)
따라서 \(\delta = \text{min(}\) \( \delta_{1}, \delta_{2} \) \(\text{)}\) 으로 설정하면
\( 0 < |x-a| < \delta \) 일 때
\( 0 < |x-a| < \delta_{1}, 0 < |x-a| < \delta_{2} \)를 동시에 만족하고
그로 인해 \( |f(x) - L| < \frac{\epsilon}{2}, |g(x) - M| < \frac{\epsilon}{2} \)를 동시에 만족하게 된다.
따라서 식 \(\text{(1)}\)에 의해
\( \begin{align} |f(x) + g(x) - (L + M)| &\le& |f(x) - L| + |g(x) - M| \\ &<& \dfrac{\epsilon}{2} + \dfrac{\epsilon}{2} = \epsilon \end{align} \)
이 성립한다.
임의의 \(\epsilon > 0\)에 대해 \( 0 < |x-a| < \delta \) \( \Longrightarrow \) \(|f(x) + g(x) - (L + M)| < \epsilon\)
을 만족하는 \( \delta > 0\)이 \(\delta = \text{min(}\) \( \delta_{1}, \delta_{2} \) \(\text{)}\) 으로 존재함을 보였으므로 극한의 정의에 의해 다음이 만족한다.
$$ \lim_{x \to a} [f(x) + g(x)] = L + M $$
\( 2. \) \(\lim\limits_{x \to a} f(x)g(x) = LM \) 증명
\(\epsilon > 0\)이 주어졌다고 하자. 다음을 만족하는 \(\delta > 0\)이 존재함을 보이면 된다.
\(\text{if } 0 < |x-a| < \delta \text{ then } |f(x)g(x) - LM| < \epsilon \)
\( |f(x) - L|, |g(x) - M| \)을 얻어내기 위해 다음과 같이 \( Lg(x) \)를 더하고 빼자.
\( \begin{align} |f(x)g(x) - LM| &=& &|f(x)g(x) - Lg(x) - LM + Lg(x)|& \\ &=& &\textcolor{red}{|}[f(x)-L]g(x) + L[g(x) - M]\textcolor{red}{|}& \\ &\le& &\textcolor{red}{|}[f(x) - L]g(x)\textcolor{red}{|} + \textcolor{red}{|}L[g(x) - M]\textcolor{red}{|}& \textcolor{red}{ (삼각부등식) } \\ &=& &|f(x) - L||g(x)| + |L||g(x) - M|& \end{align} \)
이제 각각을 \( \dfrac{\epsilon}{2} \)보다 작게 만듬으로 전체를 \( \epsilon \) 보다 작게 만들 수 있다.
한편 \(\lim\limits_{x \to a} g(x) = M \)임이 주어져 있으므로
\( 0 < |x-a| < \delta_{1} \Longrightarrow |g(x) - M| < \dfrac{\epsilon}{2(1+|L|)}\) 을 만족하는 \(\delta_{1}\)이 존재한다. (분모의 \( |L|\)에 굳이 1을 더한 이유는 \(L=0\)인 경우 분모에 들어갈 수 없게 되는 상황을 방지하기 위함이다.)
\( 0 < |x-a| < \delta_{2} \Longrightarrow |g(x) - M| < 1 \) 을 만족하는 \(\delta_{2}\) 역시 존재한다.
(정의에 의해 극한이 존재하려면 그 어떤 \(\epsilon\)에 대해서도 이에 대응하는 \(\delta\)가 존재해야 하므로 \( \epsilon\) 자리에 아무 수를 넣어도 상관없다. 여기서는 1을 넣었다.)
그리고 두 번째 식인 \( |g(x) - M| < 1 \)와 삼각부등식을 이용하면 다음이 성립한다.
\( |g(x)| = |g(x) - M + M| \) \( \le \) \(|g(x) -M|\) \(+ |M| < \) \(1\) \(+ |M|\)
또 한편 \(\lim\limits_{x \to a} f(x) = L \) 임이 주어져 있으므로
\( 0 < |x-a| < \delta_{3} \Longrightarrow |f(x) - L| < \dfrac{\epsilon}{2(1+|M|)}\) 을 만족하는 \(\delta_{3}\)이 존재한다.
이제 \(\delta = \text{min(} \delta_{1}, \delta_{2}, \delta_{3} \text{)}\) 이라 하면
\( 0 < |x-a| < \delta \) 이면 \( \begin{cases} 0 < |x-a| < \delta_{1} \\ 0 < |x-a| < \delta_{2} \\ 0 < |x-a| < \delta_{3} \end{cases} \) 이 모두 성립하므로
\( \begin{cases} |g(x) - M| < \dfrac{\epsilon}{2(1+|L|)} \\ |g(x) - M| < 1 \\ |f(x) - L| < \dfrac{\epsilon}{2(1+|M|)} \end{cases} \)가 모두 성립하게 된다.
따라서
\( \begin{align*} |f(x)g(x) - LM| &\le& &|f(x) - L||g(x)| \textcolor{red}{+} |L||g(x) - M|& \\ &<& &\dfrac{\epsilon}{2(1+|M|)}(1+|M|) \textcolor{red}{+} |L|\dfrac{\epsilon}{2(1+|L|)}& \\ &<& &\dfrac{\epsilon}{2} \textcolor{red}{+} \dfrac{\epsilon}{2}& \\ &=& &\epsilon& \end{align*}\)
이는 극한의 정의에 의해 다음이 성립함을 보여준다.
$$ \lim_{x \to a} f(x)g(x) = LM $$
\( 3. \) \(\lim\limits_{x \to a} cf(x) = cL \) 증명
2번의 증명에서 \( g(x) = c \) 라고 하면
$$ \begin{align*} \lim_{x \to a} [cf(x)] &=& &\lim_{x \to a} [g(x)f(x)]& = \lim_{x \to a} g(x) \cdot \lim_{x \to a}f(x) \\ &=& &\lim_{x \to a} c \cdot \lim_{x \to a} f(x)& \\ &=& &c\lim_{x \to a} f(x) = cL& \end{align*} $$
\( 4. \) \(\lim\limits_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{L}{M} \) 증명
위에서 증명한 곱의법칙을 이용해 \( \lim\limits_{x \to a} \dfrac{1}{g(x)} \times \lim\limits_{x \to a} f(x) = \dfrac{1}{M} \times L = \dfrac{L}{M}\)을 보일것이다.
그러기 위해서는 \( \lim\limits_{x \to a} \dfrac{1}{g(x)} = \dfrac{1}{M} \)임을 먼저 보여야 한다.
즉 임의의 \( \epsilon > 0 \)에 대해 \(\delta > 0\)가 존재하여 (\(\delta\) 존재성 보이는게 \(\epsilon - \delta \)논법의 핵심임)
\(0 < |x-a| < \delta\) \( \Longrightarrow \) \( \left|\dfrac{1}{g(x)} - \dfrac{1}{M}\right| < \epsilon \) 임을 보여야 한다.
\(\left|\dfrac{1}{g(x)} - \dfrac{1}{M}\right| = \dfrac{|M - g(x)|}{|Mg(x)|} \) 인데,
\( |M-g(x)| < \) (어떤 식), \(\dfrac{1}{Mg(x)} < \) (또 어떤 식) 을 유도해서
\( \dfrac{|M - g(x)|}{|Mg(x)|} = \) (어떤 식) \(\times\) (또 어떤 식) \(<\epsilon\) 하는 식으로
\(\epsilon\)보다 작다는것을 이끌어 낼 것이다.
여기서 분자는 \(|M - g(x)| = |g(x) - M|\)이고 \( \lim\limits_{x \to a} g(x) = M \)으로 수렴하므로
\(|g(x) - M|\)이 무언가보다 작게 해주는 \(\delta > 0\)가 존재할 것임이 바로 보인다.
하지만 \(\dfrac{1}{|Mg(x)|}\) 는 \(|g(x) - M|\) 으로 무언가보다 작다는것을 이끌어내는 방법이 바로 보이진 않는다.
그러므로 다음과 같이 시도해보자.
\(\lim\limits_{x\to a} g(x) = M\) 이므로 \(\delta_{1}>0\)이 존재하여
\(0<|x-a|< \delta_{1}\) \(\Longrightarrow \) \( |g(x) - M| < \dfrac{|M|}{2} \) (임의의 \(\epsilon\) 에 대해 성립하므로 \(\epsilon\) 자리에는 \(\frac{|M|}{2}\) 같은 아무 수나 들어갈 수 있다.)
그러므로 다음이 성립한다.
\( |M|\) \(= |M - g(x) + g(x)| \le\) \(|M-g(x)|\)\( + |g(x)| < \) \(\dfrac{|M|}{2}\)\( + |g(x)| \)
이 식에서 양변에 \(\dfrac{|M|}{2}\)를 빼주면 \( |g(x)| > \dfrac{|M|}{2} \)를 얻는다.
이는 정리하면 \(0 < |x-a| < \delta_{1} \Longrightarrow |g(x)| > \dfrac{|M|}{2} \) 임을 보여준다.
따라서 이런 \(x\)들에 대해서는
\(\dfrac{1}{|Mg(x)|}\) \(= \dfrac{1}{|M||g(x)|} \)\(<\) \(\dfrac{1}{|M|} \cdot \dfrac{2}{|M|} = \)\(\dfrac{2}{M^{2}}\) 가 성립한다.
한편 \(\delta_{2} > 0\)역시 존재하여
\(0<|x-a|< \delta_{2}\) \(\Longrightarrow \) \( |g(x) - M| < \dfrac{M^{2}}{2}\epsilon \) 를 만족하므로
\(\delta = \text{min(} \delta_{1}, \delta_{2} \text{)} \) 이라 하면
\(0< |x-a| < \delta \Longrightarrow \left|\dfrac{1}{g(x)} - \dfrac{1}{M}\right| = \dfrac{|M - g(x)|}{|Mg(x)|} < \dfrac{2}{M^{2}}\dfrac{M^{2}}{2}\epsilon = \epsilon \)
극한의 정의에 의해 \(\lim\limits_{x \to a} \dfrac{1}{g(x)} = \dfrac{1}{M}\) 임이 증명 되었다.
이제 곱의 법칙에 의해 다음이 성립한다.
$$ \lim_{x \to a} \dfrac{f(x)}{g(x)} = \lim_{x \to a} f(x) \cdot \dfrac{1}{g(x)} = \lim_{x \to a} f(x) \cdot \lim_{x \to a} \dfrac{1}{g(x)} = \dfrac{L}{M} $$
위에서 보인 극한정리를 이용하면 \(n\)이 정수일 때 다음이 성립함을 알 수 있다.
$$ \lim_{x \to a} cx^{n} = ca^{n} $$
이로써 복잡한 다항식이나 유리식의 극한을 계산할 수 있게 되었다.
극한을 계산할 때 때때로 압축 정리(내지는 스퀴즈 정리, 샌드위치 정리라고도 부른다. 모두 수학용어이다)
를 이용하는것이 도움이 될 때가 있다.
압축 정리(Squeeze Theorem)
\(a\)근처의 모든 점 \(x\)에 대해 (\(a\)는 제외 가능)
\( f(x) \le g(x) \le h(x) \) 이고 \(\lim\limits_{x \to a} f(x) = \lim\limits_{x \to a} h(x) = L\) 이 성립한다면 다음이 성립한다.
$$ \lim_{x \to a} g(x) = L $$
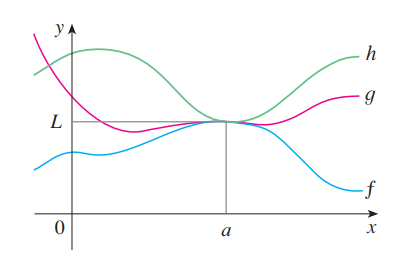
압축 정리 증명
\(\lim\limits_{x \to a} f(x) = \lim\limits_{x \to a} h(x) = L\) 이므로
임의의 \(\epsilon > 0\)에 대해
\(0 < |x-a| < \delta_{1} \Longrightarrow |f(x) - L| < \epsilon \)을 만족하는 \(\delta_{1} > 0\)이 존재하고
\(0 < |x-a| < \delta_{2} \Longrightarrow |h(x) - L| < \epsilon \)을 만족하는 \(\delta_{2} > 0\)이 존재한다.
위 식들로부터 다음 부등식을 얻는다.
\( L-\epsilon < f(x) \) 과 \( h(x) < L + \epsilon \)
\(\delta = \text{min(} \delta_{1}, \delta_{2} \text{)}\)라고 하면
\( x=a\) 근처의 점에서 \( f(x) \le g(x) \le h(x) \) 임이 주어져 있으므로 다음이 성립한다.
\( L - \epsilon\) \(<\) \(f(x) \le g(x) \le h(x)\) \(< \) \(L + \epsilon \)
이는 \( |g(x) - L| <\) \( \epsilon \)과 동치이고
극한의 정의에 의해 다음을 얻는다.
$$ \lim_{x \to a} g(x) = L $$
이제 압축정리를 이용해 다음이 성립함을 보여보자.
$$ \lim_{x \to 0} x^{2}\sin{\dfrac{1}{x}} = 0 $$
참고로 다음과 같은 극한법칙의 곱의법칙을 사용할 수 없다.
$$ \lim_{x \to 0} x^{2} \times \lim_{x \to 0} \sin{\dfrac{1}{x}} $$
왜냐하면 \( \lim\limits_{x \to 0} \sin{\dfrac{1}{x}} \)이 수렴하지 않고 진동하기 때문이다.
(이에 대한 설명은 생략한다)
하지만 \(-1 \le \sin{\dfrac{1}{x}} \le 1\)임을 이용하면
\(-x^{2} \le x^{2}\sin{\dfrac{1}{x}} \le x^{2}\)를 얻고
\( \lim\limits_{x \to 0} x^{2} = \lim\limits_{x \to 0} (-x^{2}) = 0 \) 이므로
압축정리에 의해 다음을 얻는다.
$$ \lim_{x \to 0} x^{2}\text{sin}\dfrac{1}{x} = 0 $$
다음 포스팅에서는 함수의 연속에 대해 다룰 것이다.
이전 포스팅 : 2. 극한의 엄밀한 정의, 엡실론 델타 논법(Epsilon-delta argument)
다음 포스팅 : 4. 함수의 연속과 중간값 정리 (Continuity and Intermediate Value Theorem)
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| [연습문제] 극한, \(\epsilon - \delta\)논법, 연속 (1~4) (0) | 2021.01.04 |
|---|---|
| 4. 함수의 연속과 중간값 정리 (Continuity and Intermediate Value Theorem) (0) | 2021.01.03 |
| 2. 극한의 엄밀한 정의, 엡실론 델타 논법(Epsilon-delta argument) (2) | 2021.01.02 |
| 1. 함수의 극한 (Limits of functions) (0) | 2021.01.02 |
| 들어가기 앞서서 (0) | 2021.01.02 |