
이번 글에서는 지난 글 13. 도함수 판정법, 14. 점근선 에서 다룬 내용을 이용해
함수의 그래프를 그리는 법에 대해 다룬다.
순서가 엄격히 정해진 것은 전혀 아니지만 가장 찾기 쉬운 정보부터 표시하여
곡선을 이어가는 방식으로 진행된다.
1. 정의역 확인
2. $x$ 절편, $y$ 절편 표시
3. 대칭성 확인
4. 점근선 확인
5. 증가, 감소구간 찾기
6. 극대, 극솟값이 존재하는 점 찾기
7. 오목성을 확인하고 변곡점 찾기
8. (1~7) 정보를 토대로 곡선을 그리기
각각의 과정에 대해서 따로 자세히 설명하기 보다 예제를 통해 이해하는 것이 빠르다.
예제
다음 곡선을 그리시오
$$ y = \dfrac{2x^2}{x^2 - 1} $$
1. 정의역 확인
이 함수는 유리함수이므로 분모가 $0$ 이 되지 않는 $x$ 에서 정의된다.
따라서 정의역은 다음과 같다.
$$(-\infty, -1) \cup (-1, 1) \cup (1, \infty)$$
2. $x$ 절편, $y$ 절편 표시
$x = 0$ 이면 $y = \dfrac{0}{-1} = 0$ 이므로 $y$ 절편은 $0$ 이다.
$y = 0$ 이면 $0 = \dfrac{2x^2}{x^2 - 1} \rightarrow x = 0$ 이므로 $x$ 절편은 $0$ 이다.
따라서 $(0, 0)$ 을 지난다고 그래프 위에 점으로 표시해둔다.
3. 대칭성 확인
$f(-x) = \dfrac{2x^2}{x^2-1} = f(x)$ 이므로 우함수이다.
따라서 그래프는 $y$ 축 대칭임을 알 수 있다.
4. 점근선 확인
$\displaystyle \lim_{x \to \infty} \dfrac{2x^2}{x^2 - 1} = 2$ 이므로 $y = 2$ 는 수평점근선이다.
$x = \pm 1$ 일 때 분모가 $0$ 이므로 이 점에서의 한 쪽 극한을 계산해본다.
$$ \begin{align} &\lim_{x \to -1^{-}} \dfrac{2x^2}{x^2 - 1} = \infty, \quad &\lim_{x \to -1^{+}} \dfrac{2x^2}{x^2 - 1} = -\infty \\ &\lim_{x \to 1^{-}} \dfrac{2x^2}{x^2 - 1} = -\infty, \quad &\lim_{x \to 1^{+}} \dfrac{2x^2}{x^2 - 1} = \infty \end{align} $$
따라서 $x = -1$, $x = 1$ 은 수직점근선이고 (1 ~ 4) 번까지의 정보를 토대로 아래와 같이 예비 그림을 그린다.
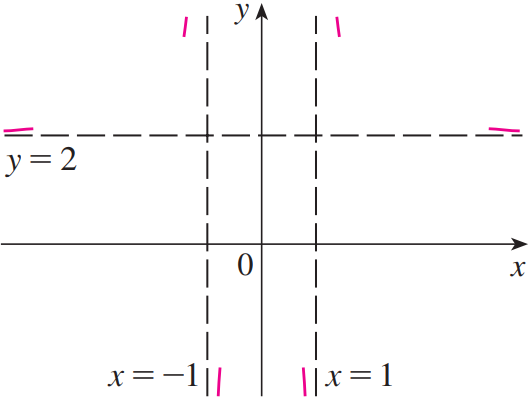
5. 증가, 감소구간 찾기
증가, 감소 구간을 찾기 위해 증가/감소 판정법을 이용할 것이다. (이 글의 증가/감소 판정법 참고)
미분을 해보면 다음과 같다.
$$ f'(x) = \dfrac{4x\cdot(x^2 - 1) - 2x^2\cdot2x}{(x^2 - 1)^2} = \dfrac{-4x}{(x^2 - 1)^2}$$
$f'(x)$ 는 분모가 $0$ 이 아니면 무조건 양수이므로 분자의 부호에 의해 음양이 결정된다.
따라서 $x < 0, \; (x \neq -1)$ 일 때 $f'(x) > 0$ 이므로 증가,
$x > 0, \; (x \neq 1)$ 일 때 $f'(x) < 0$ 이므로 감소한다.
6. 극대, 극소값이 존재하는 점 찾기
극대점, 극소점을 찾기 위해 1계도함수 판정법을 이용할 것이다. (이 글의 1계도함수 판정법 참고)
위에서 구한 $f'(x)$ 에 의해 정의역 범위 내에서 임계점은 $x = 0$ 이 유일하다.
또 $x = 0$ 을 기준으로 양에서 음으로 바뀌므로 $x= 0$ 은 유일한 극대점이다.
7. 오목성을 확인하고 변곡점 찾기
오목성을 확인하기 위해 오목성 판정법을 이용할 것이다. (이 글의 오목성 판정법 참고)
2계도함수를 구해보면 다음과 같다.
$$ f''(x) = \dfrac{12x^2 + 4}{(x^2 - 1)^3} $$
분자는 항상 양수이고
분모는 $x^2 - 1 > 0$ 인 구간, 즉 $(-\infty, -1) \cup (1, \infty)$ 에서 양수
$x^2 - 1 < 0$ 인 구간 $(-1, 1)$ 에서 음수이다.
따라서 오목성 판정법에 의해 $(-\infty, -1) \cup (1, \infty)$ 에서 위로 오목, $(-1, 1)$ 에서 아래로 오목이다.
(5 ~ 7) 번을 한번에 묶어서 다음과 같은 표를 그려보는것도 도움이 된다.
| $(-\infty, -1)$ | $-1$ | $(-1, 0)$ | $0$ | $(0, 1)$ | $1$ | $(1, \infty)$ | |
| $f(x)$ | $+$ (양수) | 정의 안 됨 | $-$ (음수) | $0$ | $-$ (음수) | 정의 안 됨 | $+$ (양수) |
| $f'(x)$ | $+$ (증가) | $+$ (증가) | $0$ (극대) | $-$ (감소) | $-$ (감소) | ||
| $f''(x)$ | $+$ (위로 오목) | $-$(아래로 오목) | $-$ (아래로 오목) | $-$ (아래로 오목) | $+$ (증가) |
8. (1 ~ 7) 정보를 토대로 곡선을 그린다.
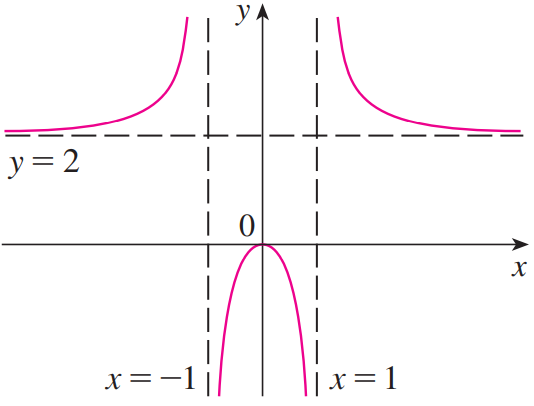
예제의 과정을 따라가며 다음 그래프도 그려보자.
$$ f(x) = \dfrac{x^3}{x^2 + 1} $$
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| [연습문제] 미분의 응용 (11~16) (0) | 2023.09.23 |
|---|---|
| 16. 역도함수(Antiderivative) (0) | 2022.12.22 |
| 14. 점근선 (Asymptote) (0) | 2022.01.07 |
| 13. 도함수 판정법 (0) | 2022.01.04 |
| 12. 롤의 정리, 평균값 정리 (Rolle's Theorem, Mean Value Theorem) (0) | 2021.02.18 |
