[연습문제] 미분의 응용 (11~16)

본 블로그의 미적분학 11번~16번 포스팅에 관한 연습문제이다.

11. 최댓값, 최솟값, 극값정리, 페르마 정리

12. 롤의 정리, 평균값 정리

13. 도함수 판정법

14. 점근선

15. 미분을 이용한 곡선 그리기

16. 역도함수

 

 

 

---

1. 다음 문장들이 참인지 거짓인지 판단하고 거짓이라면 거짓인 이유를 서술하시오.

1-1) If $f^{\prime }(c)=0$, then $f$ has a local maximum or minimum at $c$.

False.

$f(x)=x^3$ 이면 $f^{\prime }(0)=0$ 이지만 $f$ 는 $0$ 에서 극대값도 극소값도 아니다.

왜냐하면 $0$ 을 기준 $x$ 값 좌우로 $f^{\prime }(x)>0$ 이므로 $f$ 는 $x=0$ 좌우에서 증가함수이고

따라서 국소적으로 최댓값 또는 최솟값을 가질 수가 없기 때문이다.

(13. 도함수 판정법의 1계 도함수 판정법 참조)

1-2) If $f$ has an absolute minimum at $c$, then $f^{\prime }(c)=0$

False.

$f(x)=\{\begin{array}{ll}-1& \text{if }x=0\\ 1& \text{if }x\ne 0\end{array}$ 이면 $f$ 는 $0$ 에서 최솟값을 갖지만

$f^{\prime }(0)$ 가 정의되지 않으므로 $f^{\prime }(0)=0$ 이 아니다.

1-3) $f$ is continuous on $(a,b)$, then $f$ attains an absolute maximum value $f(c)$ and an absolute minimum value $f(d)$ at some numbers $c$ and $d$ in $(a,b)$.

False.

$f(x)=x^2$ 이고 구간이 $(-1,1)$ 이라 하자.

그러면 $f(x)$ 는 $x=0$ 에서 최솟값을 갖고 최댓값은 존재하지 않는다.

 

$x=0$ 에서 최솟값을 갖는 것에 대한 설명 : 

구간에 $x=-1,1$ 을 추가해서 폐구간 $[-1,1]$ 이라 하자. 폐구간 방법에 따르면,

임계수(Critical number)인 $x=0$ 과 구간의 양 끝점인 $x=-1,1$ 에서 최댓값 또는 최솟값을 갖는데,

$x=0$ 일 때 최솟값이고 $x=-1,1$ 일 때 같은 최댓값을 갖는다.

이제 $x=-1,1$ 인 점을 제외시키면 최댓값은 존재하지 않고 최솟값만 남게된다.

1-4) If $f$ is differentiable and $f(-1)=f(1)$, then there is a number $c$ such that $|c|<1$ and $f^{\prime }(c)=0$.

True.

$f$ 가 미분 가능하면 연속이므로(증명은 이 글 참조)

미분가능한 구간에 대해 따로 언급이 없는 이 함수 $f$ 는 전구간에서 미분가능하고 연속이다.

따라서 $[-1,1]$ 에서 연속이고 $(-1,1)$ 에서 미분가능하며, 조건에 의해 $f(-1)=f(1)$ 이므로

롤의 정리에 의해 $f^{\prime }(c)=0$ 인 $c\in (-1,1)$ 가 존재한다.

$c\in (-1,1)$ 은 $|c|<1$ 과 동치이므로 증명 완료

1-5) There exists a function $f$ such that $f(x)<0$, $f^{\prime }(x)<0$, and $f^{″}(x)>0$ for all $x$.

False.

$f(x)<0$ 이면 전 구간에서 음수인 함수라는 뜻이고

도함수 판정법에 의하면

$f^{\prime }(x)<0$ 이면 전 구간에서 감소, $f^{″}(x)>0$ 이면 전 구간에서 위로 오목이라는 뜻이다.

 

오목이면서 감소하는 함수는 $x\to -\mathrm{\infty }$ 에서 $\mathrm{\infty }$ 로 발산하므로 양수인 구간이 존재하게 된다.

따라서 조건을 만족하는 함수는 존재하지 않는다.

 

 

수식을 이용한 증명 : 

평균값 정리에 의해 다음을 만족하는 $c\in (a,x)$ 가 존재한다.

$$f(x)-f(a)=f^{\prime }(c)(x-a)$$

한편, $f^{″}>0$ 이므로 $f^{\prime }$ 는 증가함수이고 따라서 $f^{\prime }(a)<f^{\prime }(c)$ 이다.

즉 $f(x)-f(a)=f^{\prime }(c)(x-a)>f^{\prime }(a)(x-a)$ 이고 정리하면 $f(x)>f(a)+f^{\prime }(a)(x-a)$ 이다.

양변에 $-\mathrm{\infty }$ 극한을 적용하면 우변은 $\mathrm{\infty }$ 로 발산하므로 양수인 구간이 존재하게 된다.

1-6) If $f$ and $g$ are increasing on an interval $I$, then $f+g$ is increasing on $I$.

True.

$f,g$ 가 구간 $I$ 에서 증가한다는 말은 $I$ 에 속하는 임의의 $x_1<x_2$ 에 대해

$$\{\begin{array}{l}f(x_1)<f(x_2)\\ g(x_1)<g(x_2)\end{array}$$

를 만족한다는 말이다.

둘을 더하면

$$f(x_1)+g(x_1)<f(x_2)+g(x_2)$$

이므로 증가의 정의에 의해 참이다.

1-7) If $f$ is even, then $f^{\prime }$ is even.

False.

반례 : $f(x)=x^2$ 이라하면 $f$ 는 우함수이지만 $f^{\prime }(x)=x$ 로 기함수이다.

1-8) The most general antiderivative of $f(x)=x^{-2}$ is $$F(x)=-{\displaystyle \frac{1}{x}}+C$$

True.

${\displaystyle \frac{d}{dx}}(-{\displaystyle \frac{1}{x}})=f$ 이므로 $-{\displaystyle \frac{1}{x}}$ 는 $f$ 의 역도함수이다.

또한 이 글의 정리에 의하면 $-{\displaystyle \frac{1}{x}}$ 에 상수를 더한 것이 가장 일반적인 역도함수 꼴임을 알 수 있다.

따라서 참이다.

---

2. $3x+2\cos x+5=0$ 가 오직 하나의 실근을 갖는다는 것을 증명하여라.

1. 실근이 존재함을 증명

$f(x)=3x+2\cos x$ 라고 하자.

$x=0$ 이면 $f(0)=5>0$

$x=-\pi$ 이면 $f(-\pi )=-3\pi +3<0$ 이므로

중간값 정리에 의해 $f(c)=0$ 이 되는 $c\in (-\pi ,0)$ 가 존재한다.

 

2. 근이 하나 뿐임을 증명

$f^{\prime }(x)=3-2\sin x>0$ 이므로 $f(x)$ 는 전 구간에서 증가한다.

따라서 $x$ 축을 관통하는 점은 오직 $x=c$ 일 때 뿐이다.

---

3. 직선 $Ax+By+C=0$ 와 점 $(x_1,y_1)$ 의 가장 가까운 거리 $d$ 는 다음과 같음을 증명하여라.

$$d={\displaystyle \frac{|A{x}_1+B{y}_1+C|}{\sqrt{A^2+B^2}}}$$

1. 벡터를 이용한 풀이

직선 $Ax+By+C$ 의 수직벡터는 $\mathbb{n}=<A,B>$ 이고

직선 위의 임의의 점 $(x,y)$ 에 대해 벡터 $\mathbb{r}$ 을 $\mathbb{r}=<x_1-x,y_1-y>$ 로 정의하면

직선과의 거리 $d$ 는 다음과 같다.

$$\begin{array}{rl}d=|{\text{comp}}_{\mathbb{n}}\mathbb{r}|=& \left|{\displaystyle \frac{\mathbb{n}\cdot \mathbb{r}}{|\mathbb{n}|}}\right|\\ =& {\displaystyle \frac{|A{x}_1+B{y}_1-Ax-By|}{\sqrt{A^2+B^2}}}\\ =& {\displaystyle \frac{|A{x}_1+B{y}_1-(-C)|}{\sqrt{A^2+B^2}}}\\ =& {\displaystyle \frac{|A{x}_1+B{y}_1+C|}{\sqrt{A^2+B^2}}}\end{array}$$

 

2. 벡터를 쓰지 않는 풀이

직선 $Ax+By+C=0$ 의 기울기는 $-{\displaystyle \frac{B}{A}}$ 인데 이와 수직인 기울기는 ${\displaystyle \frac{A}{B}}$ 이다.

기울기가 ${\displaystyle \frac{A}{B}}$ 이고 점 $(x_1,y_1)$ 을 지나는 직선의 방정식은 다음과 같다.

$$y={\displaystyle \frac{A}{B}}(x-x_1)+y_1$$

이 직선과 처음의 직선 $Ax+By+C=0$ 를 연립하면 교점을 얻을 수 있는데,

이 교점과 점 $(x_1,y_1)$ 사이의 거리가 $d$ 가 된다.

계산은 복잡하므로 생략한다.

 

3. 또다른 풀이

2번 풀이에서 언급한 교점을 $(x,y)$ 라 하자. 그러면 $d^2$ 는 다음과 같다.

$$d^2=(x-x_1{)}^2+(y-y_1{)}^2$$

$(x,y)$ 는 직선 $Ax+By+C=0$ 위의 점이므로 직선식을 대입할 수 있다.

$$Ax+By+C=0⟹x=-{\displaystyle \frac{B}{A}}y-{\displaystyle \frac{C}{A}}$$

로 변형한 후 대입하면 $y$ 에 대한 2차방정식이 나온다.

미분을 이용하여 최솟값을 구하면 되는데, 역시 계산이 복잡하므로 생략한다.

 

현재 단원까지는 벡터를 배우지 않아서 복잡한 계산을 하지만

후에 벡터를 공부하면 1번 풀이와 같이 간단하게 계산해낼 수 있다.

---

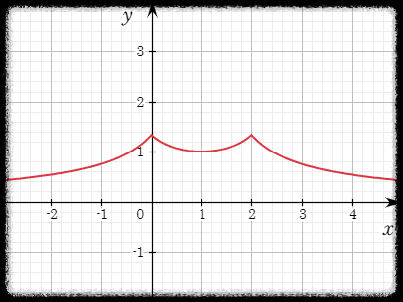
4. Find the absolute maximum value of the function

$$f(x)={\displaystyle \frac{1}{1+|x|}}+{\displaystyle \frac{1}{1+|x-2|}}$$

절댓값이 $0$ 일 때 기준으로 식이 달라지므로

$x=0,x=2$ 를 기준으로 식을 나눠서 생각해야 한다.

$$f(x)=\{\begin{array}{l}{\displaystyle \frac{1}{1-x}}+{\displaystyle \frac{1}{3-x}}\text{if }x<0\\ {\displaystyle \frac{1}{1+x}}+{\displaystyle \frac{1}{3-x}}\text{if }0\le x<2\\ {\displaystyle \frac{1}{1+x}}+{\displaystyle \frac{1}{x-1}}\text{if }2\le x\end{array}$$

정리하면

$$f(x)=\{\begin{array}{l}{\displaystyle \frac{-2(x-2)}{(x-1)(x-3)}}\text{if }x<0\\ {\displaystyle \frac{-4}{(x+1)(x-3)}}\text{if }0\le x<2\\ {\displaystyle \frac{2x}{(x+1)(x-1)}}\text{if }2\le x\end{array}$$

 

한편, $f(1+x)=f(1-x)$ 이므로 $f$ 는 $x=1$ 에 대칭이다.

편의를 위해 $x>1$ 일 때만 계산하자.

$$f^{\prime }(x)=\{\begin{array}{l}{\displaystyle \frac{8(x-1)}{(x+1{)}^2(x-3{)}^2}}>0\text{if }1\le x<2\\ {\displaystyle \frac{-2(x^2+1)}{(x+1{)}^2(x-1{)}^2}}<0\text{if }x>2\end{array}$$ 

$x=2$ 기준으로 왼쪽에서 증가하다가 오른쪽에서 감소하므로 $x=2$ 에서 극댓값을 갖는다.

반으로 자른 구간의 끝 점인 $x=1$ 에서의 함숫값은 $f(1)=1$ 이고 $f(2)={\displaystyle \frac{4}{3}}$ 이며

$x>2$ 에서는 감소하며 더 이상 극값이 없으므로 $f$ 의 최댓값은 $f(2)={\displaystyle \frac{4}{3}}$ 이다.

 

 

그래프는 다음과 같다.