
이제 함수의 넓이를 구하는 문제로 가보자.
넓이(Area)의 가장 기본적인 정의는 가로(width) $\times$ 세로(height)이다.
삼각형의 경우 사각형의 절반의 넓이를 갖고,
다각형의 경우 여러 삼각형으로 나누어 계산한 후 합하여 넓이를 구할 수 있다.

하지만 다음과 같이 곡선이 포함된 닫힌 영역의 넓이는 바로 구할 수가 없다.
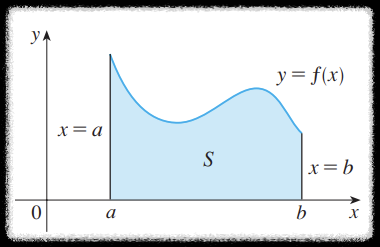
문제를 해결하기 위해 넓이를 대강 구하는 방법을 택해보자.
우선 다음과 같이 $f(x) = x^2$ 를 고려한다.

$[0, 1]$ 의 구간을 4개로 쪼개어 다음과 같이 4개의 사각형의 넓이의 합은
곡선 아래의 넓이와 대강 비슷할 것이다.

각 사각형의 높이는 각 구간의 오른쪽 끝 점 $\textcolor{limegreen}{\dfrac{1}{4}, \; \dfrac{2}{4}, \; \dfrac{3}{4}, \; 1}$ 을 택했다.
따라서 대강 구한 넓이는 다음과 같을 것이다.
$$ \text{Area} = f \left( \textcolor{limegreen}{\dfrac{1}{4}} \right) \cdot\dfrac{1}{4} + f \left( \textcolor{limegreen}{\dfrac{2}{4}} \right) \cdot\dfrac{1}{4} + f \left( \textcolor{limegreen}{\dfrac{3}{4}} \right) \cdot \dfrac{1}{4} + f \left( \textcolor{limegreen}{1}\right) \cdot\dfrac{1}{4} = 0.46875 $$
그림을 살펴보면 이 사각형들의 합은 곡선 아래 실제 넓이보다 확실히 크다.
이번엔 다음과 같이 구간의 왼쪽 끝 값을 선택하여 대강 구한 넓이의 최솟값을 찾아보자.

위와 같은 방법으로 계산해보면 $\text{Area} = 0.21875$ 를 얻을 수 있다.
따라서 실제 넓이 $\text{Area}$ 는 다음과 같은 범위를 갖는다.
$$ 0.21875 < \text{Area} < 0.46875 $$
한편 다음과 같이 구간을 8개로 쪼갠 것이 더 정확한 넓이처럼 느껴진다.

위와 같은 방법으로 계산하면 $0.3984375$ 를 얻을 수 있고
구간의 왼쪽 끝을 선택하여 넓이를 계산하면 $0.2734375$ 를 얻을 수 있다.
쪼개는 구간을 더욱 작게 하여 1000개의 구간으로 쪼개면 다음과 같이 계산된다.
$$ 0.3328335 < \text{Area} < 0.3338335 $$
넓이가 $0.3333...$ 으로 수렴해가는 것을 관찰할 수 있다.
그렇다면 실제로 무한으로 쪼개어 계산하면 $0.\dot{3}$ 이 될까?
우선 구간의 오른쪽 끝을 택하여 만든 사각형 넓이의 합을 $R_n$ 이라고 하면 다음이 성립하는지 살펴보자
$$ \lim_{n \to \infty} R_n = \dfrac{1}{3} $$
$R_n$ 을 직접 정리해보자.
$$ \begin{align} R_n = &\textcolor{limegreen}{f\left( \dfrac{1}{n} \right)} \dfrac{1}{n} + \textcolor{limegreen}{f\left( \dfrac{2}{n} \right)} \dfrac{1}{n} + \textcolor{limegreen}{f\left( \dfrac{3}{n} \right) } \dfrac{1}{n} + \cdots \textcolor{limegreen}{f\left( \dfrac{n}{n} \right)} \dfrac{1}{n} \\ = &\textcolor{limegreen}{\dfrac{1^2 + 2^2 + 3^2 + \cdots + n^2}{n^2}}\dfrac{1}{n} \\ = &(1^2 + 2^2 + 3^2 + \cdots + n^2)\dfrac{1}{n^3} \end{align} $$
여기서 $\displaystyle \sum_{k=1}^{n} k^2 = \dfrac{n(n+1)(2n+1)}{6}$ 공식을 적용하면
$$ R_n = \dfrac{(n+1)(2n+1)}{6n^2} $$
무한 극한을 적용시키면 $\dfrac{1}{3}$ 으로 실제로 수렴함을 알 수 있다.
같은 방법으로 구간의 왼쪽 끝을 택하여 만든 사각형의 넓이의 합을 $L_n$ 이라고 하면
$ \displaystyle \lim_{n \to \infty} L_n = \dfrac{1}{3} $ 임을 알 수 있다.
따라서 실제 넓이는 샌드위치 정리에 의해 $\dfrac{1}{3}$ 로 수렴한다.
위와 같은 방법으로 넓이를 구하는 것은 꽤나 적절해보인다.
수학자들은 곡면 아래 놓인 넓이를 위와 같이
구간을 쪼개어 만든 사각형들의 넓이의 합의 극한으로 정의하기로 했다.
정의
구간 $S$ 에서 연속인 함수 $f$ 아래 놓인 넓이 $A$ 는 다음과 같이
사각형들의 넓이의 합으로 구한 근사치의 극한으로 한다.
$$A = \lim_{n \to \infty} R_n = \lim_{n \to \infty} [f(x_1)\Delta x + f(x_2)\Delta x + \cdots + f(x_n)\Delta x]$$
실제로는 구간의 우측 끝 값 말고 좌측 끝 값을 이용해도 되고,
심지어 각 구간에서 구간 내의 임의의 점을 각각 택하여 넓이를 구해도 된다.
따라서 정의를 다음과 같이 수정한다.
그래프 넓이의 정의
구간 $S$ 에서 연속인 함수 $f$ 아래 놓인 넓이 $A$ 는 다음과 같이
사각형들의 넓이의 합으로 구한 근사치의 극한으로 한다.
$$A = \lim_{n \to \infty} [f(x_1^{*})\Delta x + f(x_2^{*})\Delta x + \cdots + f(x_n^{*})\Delta x]$$여기서 $x_k^{*}$ 는 $k$ 번째 구간에서 임의로 택한 점이다.

이렇게 구하는 그래프의 넓이는 다양하게 활용될 수 있다.
하나 예를 들자면,
함수가 속도함수이면 그래프의 아래에 놓인 넓이는 물체의 변위(displacement)가 된다.
함수가 무엇을 표현하냐에 따라 다양한 의미로 이용할 수 있는 이 계산 과정을
정적분이라 부르고 다음과 같이 정의한다.
정적분의 정의
$f$ 가 구간 $[a, b]$ 에서 정의된 연속함수이고,
이 구간을 $n$ 개의 같은 크기 $\Delta x = \dfrac{b-a}{n}$ 로 나누자.
각 구간의 끝 점을 $(a =) x_0, x_1, ... , x_n (= b)$ 라고 정의하고
$x_1^*, x_2^*, ... , x_n^*$ 을 각 구간에서의 임의의 점이라고 하면
함수 $f$ 의 $a$ 에서 $b$ 까지 정적분은 다음과 같이 정의한다.
$$ \int_{a}^{b} f(x) dx = \lim_{n \to \infty} \sum_{i=1}^n f(x_i^*) \Delta x $$
그리고 임의로 택한 점으로 구한 정적분이 수렴하고 모두 같은 값을 가진다면,
$f$ 는 $[a, b]$ 에서 적분가능하다고 한다.
엄밀한 정의와 다른 종류의 적분도 존재하지만, 대학 기초 미적분학에서는 다루지 않는다.
실제로는 구간의 크기가 같지 않아도 적분을 할 수 있다.
나눈 구간의 크기 중 가장 큰 구간의 극한이 $0$ 으로 수렴하기만 하면 된다.
참고로 정적분의 결과는 $x$ 에 대한 함수가 아니라 어떠한 상수값이다.
$f(x) \; dx$ 대신 $f(t) \; dt$ 또는 $f(r) \; dr$ 등 어떠한 변수를 이용해도 같은 값을 나타낸다.
위의 정의에서 적분가능한 조건을 걸어두었는데,
반대로 말하면 적분 불가능한 함수도 존재한다는 것이다.
다음 정리는 미적분학 수준에서 증명하지 않고 받아들인다.
적분 가능한 조건에 대한 정리
$f$ 가 구간 $[a, b]$ 에서 연속이거나 구간 내에서 유한개의 도약불연속점을 가질 때,
$f$ 는 구간 $[a, b]$ 에서 적분 가능하다.
다시말해, 정적분 $\int_a^b f(x) dx$ 가 존재한다.
정적분의 성질은 다음 글에서 다룬다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 19. 미적분학의 기본 정리 (The Fundamental Theorem of Calculus) (0) | 2023.09.24 |
|---|---|
| 18. 정적분의 성질 (Properties of Definite Integral) (0) | 2023.09.24 |
| [연습문제] 미분의 응용 (11~16) (0) | 2023.09.23 |
| 16. 역도함수(Antiderivative) (0) | 2022.12.22 |
| 15. 미분을 이용한 곡선 그리기 (2) | 2022.01.20 |