본론으로 들어가기 앞서 다음 두 글을 읽고 오는 것을 추천한다.
$\text{curl}$ 이 회전을 나타내는 연산자인 이유
$\text{div} $ 가 발산을 나타내는 연산자인 이유
그린 정리는 한 평면 위에서 선적분이랑 영역적분을 이어주는 정리이다.
추후에 소개할 스토크스 정리의 특수한 경우라고 할 수 있는데
바로 본론으로 들어가자면 그린 정리는 다음과 같다.
그린 정리(Green's Theorem)
곡선 $C$ 가 $xy$ 평면 위에서 양의 방향(반시계방향)이고 조각적으로 부드러우며 단순 닫힌 곡선이라고 하고
영역 $D$ 를 곡선 $C$ 에 유계된 영역이라고 하자.
영역 $D$ 를 포함한 열린 영역에서 $P$ 와 $Q$ 가 연속인 편도함수를 가지면 다음이 성립한다.
$$ \int_C P \; dx + Q \; dy = \iint_D \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA $$
증명은 미적분학 수준에서 할 수 없으므로 생략한다.
참고로 책에 나와있는 증명은 특수한 영역에서만 성립하는 것을 보여주고 있기 때문에 완벽한 증명이 아니다.
정리에서 말하는 양의 방향은 반시계 방향인데, 반대로 음의 방향은 시계 방향으로 약속한다.
그리고 앞으로 종종 나올 표현인데,
어떤 유계 영역 $D$ 에 대해 이 영역의 양의 방향의 경계를 기호로 $\partial D$ 로 쓰곤 한다.
그린 정리는 다음과 같이 생각하여 간단한 형태로 표현할 수도 있다.
$xy$ 평면에 분포하는 벡터장 $\textbf{F}(x,y,z) = <P(x,y,z), Q(x,y,z), 0>$ 과
$xy$ 평면에 놓인 곡선 $\textbf{r}(t) = <x(t), y(t), 0>$ 을 고려해보자.
그러면 $d\textbf{r} = <dx, dy, 0>$ 이고
그린 정리의 좌변은 다음과 같이 변형될 수 있다.
$$ \begin{align} \int_C P \; dx + Q \; dy = &\int_C <P,Q,0> \cdot <dx, dy, 0> \\ = &\textcolor{orange}{\int_C \textbf{F} \cdot d\textbf{r} } \end{align} $$
그리고 $\text{curl }\textbf{F} = \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \textbf{k} $ 이므로
그린 정리의 우변은 다음과 같이 쓸 수 있다.
$$ \iint_D \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA = \textcolor{orange}{\iint_D \text{curl }\textbf{F} \cdot \textbf{k} \; dA} $$
따라서 그린정리를 다음과 같이 표현할 수도 있다.
그린 정리의 벡터 표현
$$ \int_C \textbf{F} \cdot d\textbf{r} = \iint_D \text{curl }\textbf{F} \cdot \textbf{k} \; dA =
\iint_D (\nabla \times \textbf{F}) \cdot \textbf{k} \; dA $$
벡터 표현으로 정리를 살펴보면,
좌변은 경계선의 반시계 회전 방향으로의 벡터장의 성분 합을 의미하고
우변은 국소적인 회전 성분들의 영역 전체에서의 합을 의미하는데,
이 둘을 합쳐보면 다음과 같은 의미를 가진다고 할 수 있다.
주어진 전체 영역에서의 벡터장의 회전은 그 영역 경계에서의 회전이랑 같다.
(영역 전체에서 일일히 회전을 계산해서 더할 필요 없이
경계선에서의 회전만 계산하면 된다는 의미로도 해석할 수 있다.)
그린 정리는 미적분학의 기본정리의 이중적분 버전이라고 볼 수 있다.
벡터 형태로 표현된 그린 정리의 좌우를 바꿔서 적으면 다음과 같고
$$ \iint_D (\nabla \times \textbf{F}) \cdot \textbf{k} \; dA = \int_C \textbf{F} \cdot d\textbf{r} $$
미적분학의 기본정리는 다음과 같은데
$$ \int_a^b F'(x) \; dx = F(b) - F(a) $$
두 정리의 좌측이 우측보다 적분 갯수가 하나 많다는 것도 공통점이고
두 정리 모두 좌측이 미분기호와 관련되어 있다는 것도 공통점이고
두 정리 모두 우측에는 미분하기 전 원함수에 관련된 식이 있다는 것도 공통점이다.
그린 정리를 이용하면 복잡한 선적분이 있는 경우 선적분을 직접하지 않고도
면적분을 통해 그 결과를 계산할 수 있게 해준다. (물론 면적분으로도 계산이 어려워서 정리를 못 쓰는 경우도 있다.)
예제 1
곡선 $C$ 가 원 $x^2 + y^2 = 9$ 이고
벡터장이 $\textbf{F} = <3y - e^{\sin{x}}, 7x + \sqrt{y^4 + 1}, 0>$ 일 때 $ \displaystyle \oint_C \textbf{F} \cdot d\textbf{r} $ 를 계산하라
주어진 선적분을 바로 계산하기는 쉽지 않다.
그린 정리를 이용해 면적분으로는 쉽게 풀리는지 살펴보자.
그린 정리에 의해 다음이 성립한다.
$$ \oint_C \textbf{F} \cdot d\textbf{r} = \iint_D (\nabla \times \textbf{F}) \cdot \textbf{k} \; dA $$
그런데 우변의 피적분함수를 계산해봤더니 다음과 같이 간단하게 나온다.
$$ \begin{align} \textcolor{orange}{\left( \nabla \times \textbf{F} \right)} \cdot \textcolor{skyblue}{\textbf{k}} = &\textcolor{orange}{\left( \dfrac{\partial (7x + \sqrt{y^2 + 1}) }{\partial x} - \dfrac{\partial (3y - e^{\sin{x}})}{\partial y} \right) \textbf{k}} \cdot \textcolor{skyblue}{\textbf{k}} \\ = &4 \end{align} $$
적분하고자 하는 영역 $D$ 는 원이므로 극좌표계로 변환하여 다음과 같이 계산할 수 있다.
$$ \iint_D 4 \; dA = \int_0^{2\pi} \int_0^3 4 r \; dr \;d\theta = 36 \pi $$
위에서 그린 정리는 단순 연결영역에서 성립한다고 언급했는데,
그린 정리를 응용하면 다음 그림처럼 영역 가운데에 구멍이 있어 단순 연결 영역이 아닌 경우에도 이용할 수 있다.

이 영역의 경계인 두 곡선 $C_1$, $C_2$ 가 각각 반시계 방향, 시계방향이라고 가정하자.
그리고 이 영역을 다음 그림과 같이 두 개의 영역 $D'$, $D''$ 으로 나누어서 살펴보면
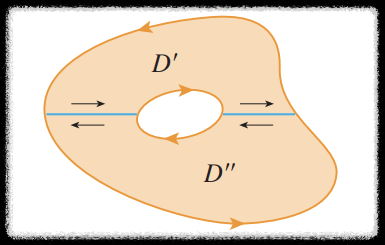
$D'$ 를 둘러싸고 있는 곡선도 반시계 방향이고 $D''$ 를 둘러싸고 있는 곡선도 반시계 방향이 된다.
그리고 전체 영역 $D$ 에서의 적분은 $D'$ 에서의 적분과 $D''$ 에서의 적분의 합과 같으니 다음과 같고
$$ \iint_D \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA = \iint_{D'} \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA + \iint_{D''} \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA $$
우변의 각 항에 그린 정리를 적용하면 다음과 같다.
($D'$ 와 $D''$ 를 나눴던 이유가 그린 정리를 적용하기 위해선 각각이 단순 연결영역이어야 하기 때문이다.)
$$ = \int_{\partial D'} \textbf{F} \cdot d\textbf{r} + \int_{\partial D''} \textbf{F} \cdot d\textbf{r} $$
그런데 위 그림에서 파란 선에 해당하는 부분에서 두 경계선은 방향이 서로 반대이므로
이 부분에서의 선적분 값은 상쇄되어 없어지고 곡선 $C_1$ 와 $C_2$ 에서의 선적분만 남게 된다.
따라서 다음과 같다.
$$ \iint_D \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial y} \right) \; dA = \int_{C_1} \textbf{F} \cdot d\textbf{r} + \int_{C_2} \textbf{F} \cdot d\textbf{r} $$
요약하면 구멍이 있는 영역에서 그린 정리를 적용하면
전체 영역을 둘러싸는 큰 곡선과 구멍을 둘러싸는 작은 곡선에서의 선적분의 합으로 표현할 수 있다는 것이다.
(단, 큰 곡선에서는 반시계 방향, 작은 곡선에서는 시계 방향)
예제 2
벡터장이 다음과 같이 주어져 있을 때
$$ \textbf{F} = \dfrac{<-y, x>}{x^2 + y^2} $$
원점 주위를 둘러싸는 양의 방향을 갖는 임의의 단순 폐곡선 $C$ 에 대해
다음이 성립함을 보여라.
$$ \int_C \textbf{F} \cdot d\textbf{r} = 2\pi $$
$C$ 가 식으로써 제시된 곡선이 아니고 임의의 곡선이므로 주어진 선적분은 계산할 수 없다.
그럼 그린 정리를 이용해볼까 고려할 수 있는데,
만약 영역 $D$ 를 단순히 폐곡선 $C$ 가 유계하고 있는 영역으로 설정한다면 문제가 생긴다.
원점에서 $\textbf{F}$ 의 분모가 $0$ 이 되므로 벡터장이 정의되지 않고
따라서 원점에서 $\dfrac{\partial Q}{\partial x}$ 나 $\dfrac{\partial P}{\partial y}$ 가 정의되지 않기 때문이다.
이 것을 피하기 위해 폐곡선 $C$ 의 유계영역 안에 모두 들어갈만큼 아주 작은 반지름 $a$ 을 갖는
원 형태의 곡선 $C'$ 를 추가하자. 여기서 $C'$ 의 방향은 반시계 방향으로 설정한다.
(시계 방향으로 설정해도 상관 없긴 하다.)
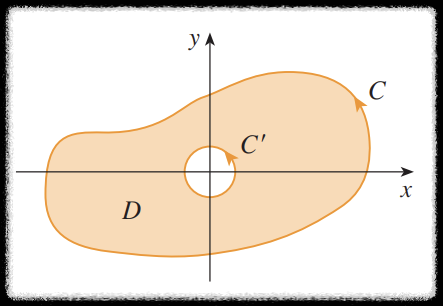
이제 위에서 설명한 구멍이 있는 영역에서의 그린정리를 이용하면 다음과 같다.
$$ \begin{align} \int_C \textbf{F} \cdot d\textbf{r} + \int_{-C'} \textbf{F} \cdot d\textbf{r} = &\iint_{D} \left( \dfrac{\partial Q}{\partial x} - \dfrac{\partial P}{\partial x} \right) \; dA \\ = &\iint_D \left[ \dfrac{y^2 - x^2}{(x^2 + y^2)^2} - \dfrac{y^2 - x^2}{(x^2 + y^2)^2} \right] \; dA = 0 \end{align} $$
즉 다음이 성립한다.
$$ \textcolor{orange}{\int_C \textbf{F} \cdot d\textbf{r}} = -\int_{-C'} \textbf{F} \cdot d\textbf{r} = \textcolor{orange}{\int_{C'} \textbf{F} \cdot d\textbf{r}} $$
그런데 $ \displaystyle \int_{C'} \textbf{F} \cdot d\textbf{r} $ 은
곡선 $C'$ 가 반지름이 $a$ 인 원이라고 주어져 있었으므로 계산이 가능하다.
$C : \textbf{r}(t) = <a\cos{t}, a\sin{t}>$ 라고 하면
$$ \begin{align} \int_{C'} \textbf{F} \cdot d\textbf{r} = &\int_{0}^{2\pi} \textbf{F}(a\cos{t}, a\sin{t}) \cdot <-a\sin{t}, a\cos{t}> \; dt \\ = &\int_{0}^{2\pi} \dfrac{a^2\cos^2{t} + a^2\sin^2{t}}{a^2\cos^2{t} + a^2\sin^2{t}} \; dt \\ = &\int_0^{2\pi} 1 \; dt = 2\pi \end{align} $$
따라서 $ \displaystyle \int_C \textbf{F} \cdot d\textbf{r} = 2\pi$ 이다.
예제 3 (연세대학교 편입학 2021년 기출)
곡선 $C$ 는 타원 $\dfrac{x^2}{2} + \dfrac{y^2}{6} = 1$ 을 따라서
$(1, \sqrt{3})$ 부터 $(1, -\sqrt{3})$ 까지 반시계 방향으로 이동하는 단순 곡선이다.
벡터장 $\textbf{F} = \dfrac{<-y, x>}{\sqrt{x^2 + y^2}}$ 에 대해 선적분 $\displaystyle \int_C \textbf{F} \cdot d\textbf{r}$ 을 구하라.
우선 이 문제는 선적분의 기본정리를 이용해 풀 수 없다.
$f(x,y) = \tan^{-1}{\left( \frac{y}{x} \right)}$ 라고 하자.
$$ \begin{cases} \dfrac{\partial f}{\partial x} = \dfrac{-\dfrac{y}{x^2}}{1 + \left( \dfrac{y}{x} \right)^2} = \dfrac{-y}{x^2 + y^2} \\ \dfrac{\partial f}{\partial y} = \dfrac{\dfrac{1}{x}}{1 + \left( \dfrac{y}{x} \right)^2} = \dfrac{x}{x^2 + y^2} \end{cases} $$
이므로 $\nabla f = \textbf{F}$ 가 성립하고 따라서 $f$ 는 $\textbf{F}$ 의 포텐셜 함수라고 생각했다면 틀렸다.
왜냐하면 $\tan^{-1}{ \left( \frac{y}{x} \right) }$ 는 애초에 $x = 0$ 에서 정의가 안되는 함수이기 때문이다.
정확히는 $y$ 축 왼쪽 또는 오른쪽 각각의 영역에 대해서는 포텐셜 함수가 맞기는 하고
선적분할 때 경로가 $y$ 축을 넘나드는 일이 없기만 하다면 (그래서 $x = 0$ 인 경우를 피하면)
$\tan^{-1}{\left( \frac{y}{x} \right)}$ 를 포텐셜 함수로 간주해 선적분의 기본정리를 적용해 풀 수 있기는 하다.
이 문제의 경우에는 다음 그림과 같이 곡선 $C$ 가 $y$ 축을 넘나들었기 때문에 문제가 생긴다.
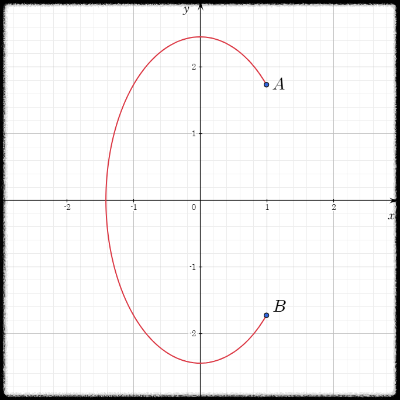
이 곡선을 포함하는 영역을 아무리 잘 잡아보려고 해도 $y$ 축은 무조건 넘나들게 된다는 것을 알 수 있다.
따라서 $\tan^{-1}{\left( \frac{y}{x} \right)}$ 는 이 문제에서 주어진 벡터장의 포텐셜 함수가 될 수 없다.
대신 다음과 같은 방법을 생각해볼 수 있다.
두 점 $A : (1, \sqrt{3})$, $B : (1, -\sqrt{3})$ 를 이은 선분을 다음과 같이 정의하자.
$$ C_1 : \textbf{r}(t) = <1, \;t>, \quad -\sqrt{3} \le t \le \sqrt{3} $$
그러면 $C \cup C_1$ 은 반시계 방향의 폐곡선을 이룬다.
그리고 내부에 충분히 작은 반지름 $a$ 를 갖는 반시계 방향 원을 그리고 이 곡선을 다음과 같이 정의하자.
$$ C_2 : \textbf{r}(t) = <a\cos{t}, \; a\sin{t}>, \quad 0 \le t \le 2\pi $$
이 두 폐곡선 사이에 존재하는 영역을 $D$ 라고 하자.
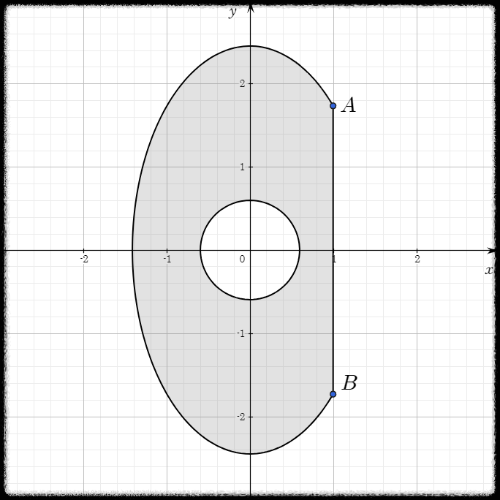
주어진 벡터장을 $\textbf{F} = <P, \; Q>$ 라고 표현하면, 영역 $D$ 에서 $Q_y - P_x = 0$ 이므로
위에서 설명한 그린정리의 응용을 이용하면 다음과 같다.
$$ \begin{align} \iint_D Q_y - P_x \; dA = 0 = \oint_{C \cup C_1} \textbf{F} \cdot d\textbf{r} + \oint_{-C_2} \textbf{F} \cdot d\textbf{r} \\ \textcolor{red}{\Longrightarrow} \oint_{C \cup C_1} \textbf{F} \cdot d\textbf{r} = \oint_{C_2} \textbf{F} \cdot d\textbf{r} \end{align} $$
우리가 구해야 할 것은 $\displaystyle \int_{C} \textbf{F} \cdot d\textbf{r}$ 이므로 이에 대해 정리해주면 다음과 같다.
$$ \int_C \textbf{F} \cdot d\textbf{r} = \textcolor{orange}{\oint_{C_2} \textbf{F} \cdot d\textbf{r}} - \textcolor{skyblue}{\int_{C_1} \textbf{F} \cdot d\textbf{r}} $$
우변을 각각 계산해보면 다음과 같다.
$$ \textcolor{orange}{\oint_{C_2} \textbf{F} \cdot d\textbf{r}} = \int_0^{2\pi} \dfrac{<-a\sin{t}, \; a\cos{t}>}{a^2} \cdot <-a\sin{t}, \; a\cos{t}> \; dt = \int_0^{2\pi} 1 \; dt = \textcolor{orange}{2\pi} $$
$$ \textcolor{skyblue}{\int_{C_1} \textbf{F} \cdot d\textbf{r}} = \int_{-\sqrt{3}}^{\sqrt{3}} \dfrac{<-t, \; 1>}{1 + t^2} \cdot <0, \; 1> \; dt = \int_{-\sqrt{3}}^{\sqrt{3}} \dfrac{1}{1 + t^2} \; dt = \left[ \tan^{-1}{t} \right]_{-\sqrt{3}}^{\sqrt{3}} = \textcolor{skyblue}{\dfrac{2}{3}\pi} $$
$$ \therefore \textcolor{royalblue}{\int_{C} \textbf{F} \cdot d\textbf{r}} = 2\pi - \dfrac{2}{3}\pi = \textcolor{royalblue}{\dfrac{4}{3}\pi} $$
위에서 소개한 그린정리는
경계선에서의 회전정도와 영역 전체에서의 회전 합이 같다는 의미를 가지는 정리였다.
(후에 알게 되겠지만, 그린 정리는 스토크스 정리의 특수한 경우에서의 정리이다.)
이번에는 경계선에서의 발산 정도가 영역 전체에서의 발산 합이랑 같음을 의미하는
발산 그린 정리를 소개한다. (후에 배우게 될 발산 정리의 2차원 버전이다.)
발산에 관한 그린 정리
$$ \oint_C \textbf{F} \cdot \textbf{n} \; ds = \iint _D \nabla \cdot \textbf{F} \; dA $$
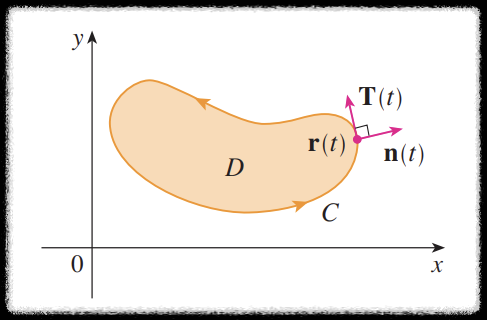
회전에 관한 그린 정리는 다음과 같았었다.
$$ \oint_C \textbf{F} \cdot d\textbf{r} = \iint_D (\nabla \times \textbf{F}) \cdot \textbf{k} \; dA $$
$ \displaystyle \oint_C \textbf{F} \cdot d\textbf{r} = \oint_C \textbf{F} \cdot \textbf{T} \; ds $ 이므로
좌변은 $C$ 의 접선 방향($\textbf{T}(t)$ 방향) 으로의 벡터장 $\textbf{F}$ 의 성분 합을 의미한다.
이번에는 접선 방향이 아닌 수직 방향($ \textbf{n}(t) $) 으로의 $\textbf{F}$ 의 성분 합을 찾아보자.
경계선에서 벡터장들이 얼마나 바깥으로 빠져 나가는가를 측정하겠다는 의미이고
$ \displaystyle \oint_C \textbf{F} \cdot \textbf{n} \; ds $ 를 계산하겠다는 말이다.
$\textbf{T}$ 가 다음과 같이 표현되는데
$$ \textbf{T}(t) = \left< \dfrac{x'(t)}{|\textbf{r}'(t)|} , \dfrac{y'(t)}{|\textbf{r}'(t)|} \right> $$
$\textbf{n}$ 은 $\textbf{T}$ 방향을 시계 방향으로 $90^{\circ}$ 회전 시킨 것이므로 다음과 같다.
$$ \textbf{n} = \begin{bmatrix} 0 & 1 \\ -1 & 0 \end{bmatrix} \begin{bmatrix} \dfrac{x'(t)}{|\textbf{r}'(t)|} \\ \dfrac{y'(t)}{|\textbf{r}'(t)|} \end{bmatrix} = \left< \dfrac{y'(t)}{|\textbf{r}'(t)|}, -\dfrac{x'(t)}{|\textbf{r}'(t)|} \right> $$
이를 대입하면 $\displaystyle \oint_C \textbf{F} \cdot \textbf{n} \; ds$ 는 다음과 같다.
$$ \begin{align} \textcolor{orange}{\oint_C \textbf{F} \cdot \textbf{n} \; ds} = &\int_a^b (\textbf{F} \cdot \textbf{n})(t) |\textbf{r}'(t)| \; dt \\ = &\int_a^b \left[ \dfrac{Py'}{|\textbf{r}'|} - \dfrac{Qx'}{|\textbf{r}'|} \right] |\textbf{r}'| \; dt \\ = &\int_a^b Py'\;dt - Qx'\;dt \\ = &\int_C P\; dy - Q\; dx = \iint_D \left( \dfrac{\partial P}{\partial x} + \dfrac{\partial Q}{\partial y} \right) \; dA = \textcolor{orange}{\iint_D \nabla \cdot \textbf{F} \; dA} \end{align} $$
마지막 줄에서 그린 정리를 이용하였다.
좌변은 경계선 $C$ 에서 벡터장 $\textbf{F}$ 의 바깥 방향 성분들의 합을 의미하고
우변에서는 $\nabla \cdot \textbf{F} = \text{div }\textbf{F}$ 이므로, 우변은 영역 $D$ 에서의 $\textbf{F}$ 의 발산의 합을 의미한다.
둘을 합쳐보면, 영역에서의 전체 발산은 경계선에서의 발산과 같다라는 의미가 된다.
(즉, 영역 전체의 발산을 일일히 계산할 필요 없이 경계선에서만 따져봐도 된다는 의미다.)
그린 정리를 응용하면 신발끈 공식도 유도할 수 있는데 설명이 길기 때문에 따로 글을 써서 정리하였다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 스칼라 함수의 면적분(Surface Integrals on Scalar Functions) (0) | 2023.10.18 |
|---|---|
| 매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas) (0) | 2023.10.17 |
| 벡터의 회전(Curl)과 발산(Div) (Curl and Divergence of Vectors) (0) | 2023.10.11 |
| 선적분의 기본정리 (Fundamental Theorem for Line Integrals) (0) | 2023.10.08 |
| 벡터장에서의 선적분 (Line Integral on Vector Fields) (0) | 2023.10.07 |