앞서 선적분에 대해 소개한 바가 있다.
원활한 이해를 위해 아래 글들을 한 번 읽고 오는 것을 추천한다.
선적분이 매개변수로 표현된 곡선을 경로 삼아 함수를 적분하는 것이였다면,
이번에 소개할 면적분은 매개변수로 표현된 곡면을 적분 영역 삼아 함수를 적분하는 것이다.
선적분에서 스칼라 함수(스칼라장)의 선적분, 벡터 함수(벡터장)의 선적분 두 종류 있었 듯이
면적분에도 스칼라 함수(스칼라장)의 면적분, 벡터 함수(벡터장)의 면적분 두 종류를 다룬다.
이번 글에서는 스칼라 함수의 면적분에 대해 다룬다.
우선 이해를 돕기 위해 잠시 선적분을 복습하고 넘어가자.
삼변수 스칼라 함수의 선적분은 다음과 같이 표현되었음을 떠올리자
$$ \int_C f(x,y, z) \; ds $$
여기서 곡선 $C$ 는 다음과 같이 표현되는 벡터함수이고
$$ \textbf{r}(t) = <x(t), \; y(t), \; z(t)> $$
$ds$ 는 이 곡선의 미소 길이이며 다음과 같이 표현할 수 있었다.
$$ \textcolor{skyblue}{ds} = \sqrt{dx^2 + dy^2 + dz^2} = \sqrt{\left( \dfrac{dx}{dt} \right)^2 + \left( \dfrac{dy}{dt} \right)^2 + \left( \dfrac{dz}{dt} \right)^2 } \; dt = \textcolor{skyblue}{|\textbf{r}'(t)| \; dt} $$
따라서 선적분 식을 매개변수인 $t$ 에 대해 표현하면 다음과 같이 표현할 수 있었다.
$$ \int_C f(x,y,z) \; \textcolor{skyblue}{ds} = \int_{t_a}^{t_b} f(\textbf{r}(t)) \textcolor{skyblue}{|\textbf{r}'(t)| \; dt} $$
비슷하게 삼변수 스칼라 함수의 면적분은 다음과 같이 적는다.
$$ \iint_S f(x,y,z) \; dS $$
여기서 곡면 $S$ 는 다음과 같이 표현되는 벡터함수이고
$$ \textbf{r}(u, v) = <x(u,v), \; y(u, v), \; z(u,v)> $$
$dS$ 는 이 곡선의 미소 면적이며 다음과 같이 표현할 수 있다. (이 글의 매개변수 곡면의 넓이 파트 참조)
$$ \textcolor{skyblue}{dS} = \textcolor{skyblue}{|\textbf{r}_u(u, v) \times \textbf{r}_v(u, v)| \; du dv} $$
따라서 면적분 식을 매개변수인 $u, v$ 에 대해 표현하면 다음과 같다.
$$ \iint_S f(x,y,z) \; \textcolor{skyblue}{dS} = \iint_D f(\textbf{r}(u,v)) \textcolor{skyblue}{|\textbf{r}_u \times \textbf{r}_v| \; du dv} $$
좌변에는 적분 영역이 $S$ 였는데 우변에서는 $D$ 로 바뀐 것에 대해 의문을 가질 수 있다.
좌변은 적분 변수가 미소 곡면 $dS$ 이므로
적분하고자 하는 범위가 곡면 위에 놓인 영역이라서 $S$ 라고 표현을 한 것이고
우변은 적분 변수가 미소 넓이 $dA = du dv$ 이므로
적분하고자 하는 범위가 곡면이 아닌 $u v$ 평면 위에 놓인 영역이라서 다르게 표현하고자 $D$ 를 쓴 것이다.
치환 적분을 할 때, 새로운 변수에 대해 적분 구간을 새로 써주는 것과 같은 이치이다.
한편, 면적분에서 피적분함수가 $f(x,y,z) = 1$ 이라면 식은 다음과 같이 쓰여지고
$$ \iint_S 1 \; dS = \iint_D |\textbf{r}_u \times \textbf{r}_v| \; dA $$
이 글에서 보았듯 이는 곡면 $S$ 의 넓이를 나타내는 식이다.
예제 1
곡면 $S$ 가 $z = x + y^2, \; 0 \le x \le 1, \; 0 \le y \le 2$ 일 때
다음 면적분을 계산하라
$$ \iint_S y \; dS $$
$u, v$ 얘기하다가 갑자기 $x, y$ 얘기가 나왔다고 해서 당황할 필요가 없다.
단지 $u, v$ 대신 $x, y$ 를 썼다는 관점으로 바라본다면
곡면의 $x$ 성분은 그냥 $x$
곡면의 $y$ 성분도 그냥 $y$
곡면의 $z$ 성분은 $x + y^2$ 로 표현되었다고 볼 수 있고
따라서 주어진 곡면을 $x, y$ 에 대한 벡터함수로 다음과 같이 표현할 수 있을 것이다.
$$ \textbf{r}(x, y) = <x, \; y, \; x + y^2> $$
미분해보면 $\textbf{r}_x$, $\textbf{r}_y$ 는 각각 다음과 같고
$$ \begin{cases} \textbf{r}_x = <1, \; 0, \; 1> \\ \textbf{r}_y = <0, \; 1, \; 2y> \end{cases} $$
이 둘을 외적하면
$$ \textbf{r}_x \times \textbf{r}_y = <-1, \; -2y, \; 1> $$
마지막으로 절댓값을 씌워주면 다음과 같이 계산 된다.
$$ |\textbf{r}_x \times \textbf{r}_y| = \sqrt{2 + 4y^2} $$
이를 대입하면 주어진 면적분을 계산할 수 있다.
$$ \begin{align} \iint_S y \; dS = &\iint_D y |\textbf{r}_x \times \textbf{r}_y| \; dA \\ = &\int_0^1 \int_0^2 y\sqrt{2+4y^2} \; dydx \\ = &\int_0^1 \int_2^{18} \dfrac{1}{8}\sqrt{k} \; dkdx = \textcolor{royalblue}{\dfrac{13\sqrt{2}}{3}} \end{align} $$
예제 2
곡면 $S$ 가 다음 세 곡면으로 유계된 영역의 경계일 때
$$ \begin{cases} y^2 + z^2 = 9 \\ x=0 \\ x+y=5 \end{cases} $$
다음 면적분을 계산하라
$$ \iint_S xz \; dS $$
이해를 돕기 위해 곡면의 그림을 그려보면 다음과 같다.
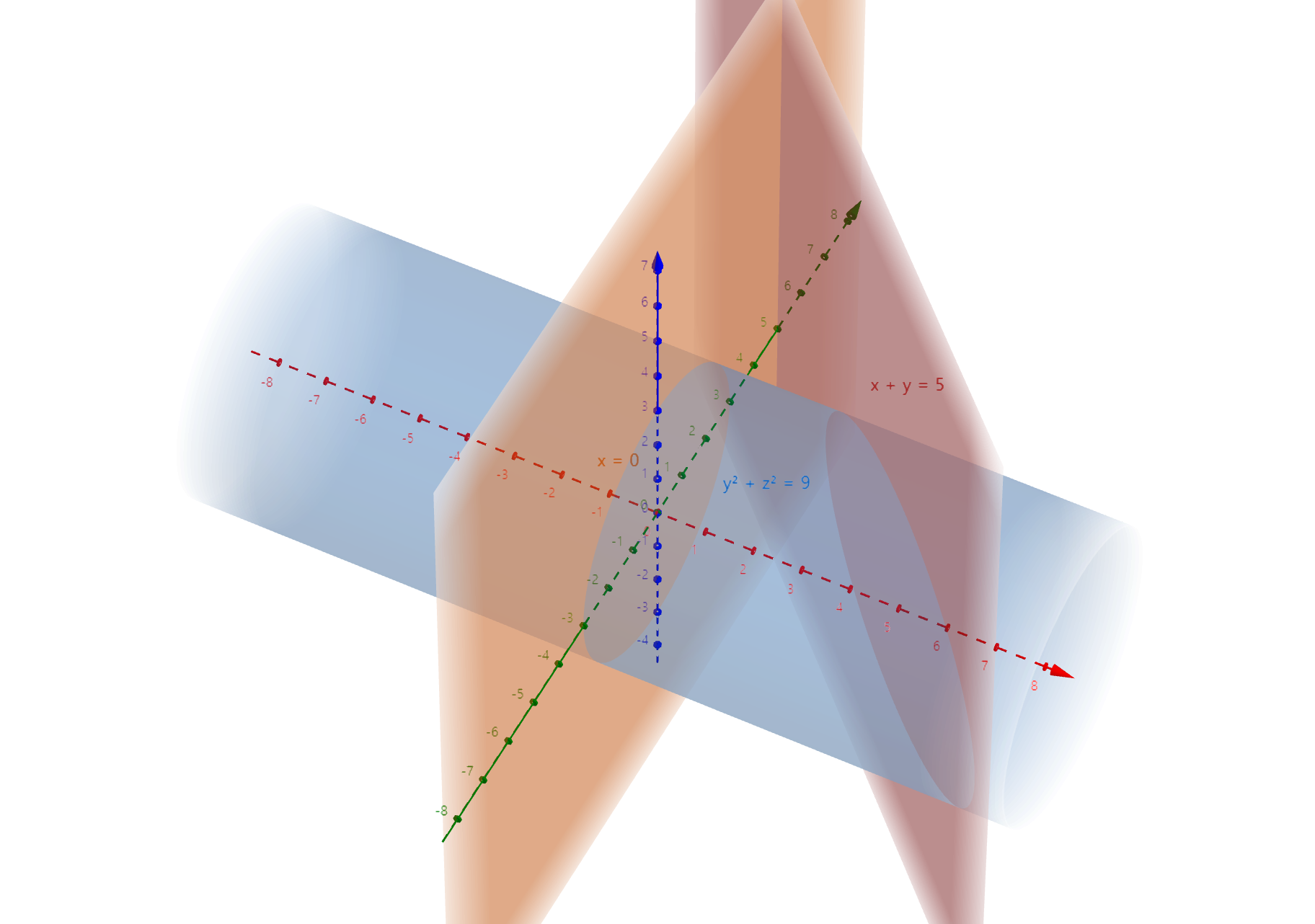
위 그림에서 보이듯 $S$ 는 다음과 같이 세 곡면 $S_1, S_2, S_3$ 으로 이루어져있다.
1. $S_1$ : 잘린 원통의 밑면 (그림에서 주황 면과 푸른 원통이 만나서 생기는 원형 면)
2. $S_2$ : 잘린 원통의 옆면
3. $S_3$ : 잘린 원통의 비스듬히 잘린 윗면 (그림에서 빨간 면과 푸른 원통이 만나서 생기는 타원형 면)
각 곡면에 대해 각각 면적분을 한 후 더해주면 요구하는 $S$ 위에서의 면적분을 계산하게 되는 것이다.
1. 잘린 원통의 밑면
원형 영역이므로 원통 좌표계를 이용하면 편할 것이다.
우선 곡면 $S_1$ 을 다음과 같이 $r, \theta$ 에 대한 매개 곡면으로 표현하자.
$$ S_1 : \textbf{r}(r, \theta) = <0, \; r\cos{\theta}, \; r\sin{\theta}>, \quad 0 \le r \le 3, \quad 0 \le \theta \le 2\pi $$
한편, $f(x,y) = xz$ 라고 하면 계산해야하는 식은 다음과 같은데
$$ \iint_{S_1} xz \; dS = \iint_D f(\textbf{r}(r, \theta)) |\textbf{r}_r \times \textbf{r}_{\theta}| \; dA $$
$ f(\textbf{r}(r, \theta)) = xz= (0)(r\sin{\theta}) = 0 $ 이므로 적분을 계산할 필요도 없이 $0$ 임을 알 수 있다.
(사실 방금 곡면 $S_1$ 을 표현할 필요도 없이 $S_1$ 의 $x$ 성분이 $0$ 이므로
피적분 함수인 $xz$ 가 $0$ 이 되는걸 알 수 있지만, 곡면을 어떻게 표현할지 모를 독자를 위해 굳이 적어보았다.)
$$ \therefore \iint_{S_1} xz \; dS = 0 $$
2. 잘린 원통의 옆면
원통 옆면의 방정식이 $y^2 + z^2 = 9$ 이므로 $y, z$ 를 다음과 같이 두자.
$$ \begin{cases} y = 3\cos{\theta} \\ z = 3\sin{\theta} \end{cases} $$
이 때 $x$ 값은 원통의 방정식인 $y^2 + z^2 = 9$ 에 의존하지 않는 변수이므로 그냥 새로운 변수로써 둘 수 있다.
하지만 원통이 잘려 있으므로 곡면 $S_2$ 의 $x$ 범위는 제한되어 있는데,
그림에서 보듯 $x$ 는 $0$ 부터 $5-y$ 까지 제한되어 있다.
위에서 $y = 3\cos{\theta}$ 로 표현하기로 했으므로 이를 이용하면 $x$ 의 범위를 다음과 같이 쓸 수 있다.
$$ 0 \le x \le 5-3\cos{\theta} $$
이를 모두 고려하면 원통의 옆면인 곡면 $S_2$ 는 다음과 같은 매개 곡면으로 표현할 수 있다.
$$ S_2 : \textbf{r}(\theta, x) = <x, \; 3\cos{\theta}, \; 3\sin{\theta}>, \quad 0 \le x \le 5-3\cos{\theta}, \quad 0 \le \theta \le 2\pi $$
이 벡터함수의 $x, \theta$ 에 대한 편미분은 다음과 같이 계산된다.
$$ \begin{cases} \textbf{r}_x = <1, \; 0, \; 0> \\ \textbf{r}_{\theta} = <0, \; -3\sin{\theta}, \; 3\cos{\theta}> \end{cases} $$
둘을 외적하면 다음과 같고
$$ \textbf{r}_x \times \textbf{r}_{\theta} = <0, \; -3\cos{\theta}, \; -3\sin{\theta}> $$
이 벡터의 크기를 구해주면 다음과 같다.
$$ |\textbf{r}_x \times \textbf{r}_{\theta}| = 3 $$
이를 이용하여 면적분을 계산해 보자.
$$ \begin{align} \iint_{S_2} xz \; dS = &\iint_D x(3\sin{\theta}) (3) \; dx d \theta \\ = &\int_0^{2\pi} \int_0^{5-3\cos{\theta}} 9x \sin{\theta} \; dx d \theta \\ = &\int_0^{2\pi} \dfrac{9}{2}\sin{\theta} (9\cos^2{\theta} -30\cos{\theta} + 25) \; d\theta \end{align} $$
여기서 $\cos{\theta} = t$ 로 치환하면 적분 구간이 $[0, 0]$ 이 되므로 적분 결과는 $0$ 임을 바로 알 수 있다.
$$\therefore \iint_{S_2} xz \; dS = 0 $$
3. 잘린 원통의 비스듬히 잘린 윗면
이 곡면($S_3$) 은 $x = 5-y$ 위에 놓여 있으므로 다음과 같은 매개 곡면으로 표현할 수 있다.
$$ \textbf{r}(y, z) = <5-y, \; y, \; z> $$
$y, z$ 에 대한 편미분은 다음과 같고
$$ \begin{cases} \textbf{r}_y = <-1, \; 1, \; 0> \\ \textbf{r}_z = <0, \; 0, \; 1> \end{cases} $$
둘을 외적하면
$$ \textbf{r}_y \times \textbf{r}_z = <1, 1, 0> $$
그리고 이 벡터의 크기는 다음과 같다.
$$ |\textbf{r}_y \times \textbf{r}_z| = \sqrt{2} $$
이를 이용하여 면적분을 계산해 보자.
$$ \begin{align} \iint_{S_3} xz \; dS = &\iint_D (5-y)z(\sqrt{2}) \; dydz \\ = &\int_{0}^{2\pi} \int_{0}^{3} \sqrt{2}(5-r\cos{\theta})r\sin{\theta} \; rdrd\theta \\ = &\sqrt{2} \int_0^{2\pi} \int_0^3 5r^2\sin{\theta} - r^3\sin{\theta}\cos{\theta} \; dr d\theta \\ = &\sqrt{2}\int_0^{2\pi} 45\sin{\theta} - \dfrac{81}{4}\sin{\theta}\cos{\theta} \; d\theta \\ = &\sqrt{2}\int_0^{2\pi} 45\sin{\theta} - \dfrac{81}{8}\sin{2\theta} \; d\theta = 0 \end{align} $$
(여기서 두 번째 줄로 넘어갈 때 $y = r\cos{\theta}, \; z = r\sin{\theta}$ 로 치환하는 변수변환을 이용했다.)
$$ \therefore \iint_{S_3} xz \; dS = 0 $$
따라서 답은 다음과 같다.
$$ \begin{align} \iint_{S} xz \; dS = &\iint_{S_1} xz \; dS + \iint_{S_2} xz \; dS + \iint_{S_3} xz \; dS \\ = &0 + 0 + 0 \\ = & 0 \end{align} $$
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 스토크스 정리(Stokes' Theorem) (0) | 2023.10.20 |
|---|---|
| 벡터 함수의 면적분(Surface Integrals on Vector Fields) (0) | 2023.10.19 |
| 매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas) (0) | 2023.10.17 |
| 그린 정리와 그 의미(Green's Theorem) (0) | 2023.10.14 |
| 벡터의 회전(Curl)과 발산(Div) (Curl and Divergence of Vectors) (0) | 2023.10.11 |