본 블로그의 미적분학 시리즈를 순서대로 보지 않고 검색을 통해 들어왔다면
다음 글들을 읽어보고 이 글을 보는 것을 추천한다.
이해를 돕기 위해 벡터장에서의 선적분을 먼저 빠르게 복습해보자.
삼변수 벡터함수의 선적분은 다음과 같은 형태를 하고 있었음을 떠올리자.
$$ \int_C \textbf{F} \cdot \textcolor{skyblue}{d\textbf{r}} = \int_C \textbf{F} \cdot \textcolor{skyblue}{\textbf{T} \; ds} $$
그리고 이는 곡선 $C$ 의 각 부분마다 곡선이 향하는 방향으로의 벡터장 $\textbf{F}$ 의 성분을 다 더한다는 의미였었다.
곡선 $C$ 는 다음과 같이 표현되는 벡터함수이고
$$ \textbf{r}(t) = <x(t), \; y(t), \; z(t)> $$
$ds$ 는 곡선의 미소 길이이므로 다음과 같이 표현할 수 있었다.
$$ \textcolor{skyblue}{ds} = \sqrt{dx^2 + dy^2 + dz^2} = \sqrt{ \left( \dfrac{dx}{dt} \right)^2 + \left( \dfrac{dy}{dt} \right)^2 + \left( \dfrac{dz}{dt} \right)^2 } = \textcolor{skyblue}{|\textbf{r}'(t)| \; dt} $$
그리고 곡선의 접선 방향을 나타내는 단위 접선벡터인 $\textbf{T}$ 는 다음과 같이 정의되므로
$$ \textcolor{skyblue}{\textbf{T}} = \textcolor{skyblue}{\dfrac{\textbf{r}'(t)}{|\textbf{r}'(t)|}} $$
$\displaystyle \int_C \textbf{F} \cdot \textbf{T} \; ds$ 를 다음과 같이 매개변수 $ t $ 에 관한 적분으로 표현할 수 있다.
$$ \int_C \textbf{F} \cdot \textcolor{skyblue}{\textbf{T} \; ds} = \int_{t_a}^{t_b} \textbf{F}(\textbf{r}(t)) \cdot \dfrac{\textbf{r}'(t)}{\cancel{|\textbf{r}'(t)|}} \cancel{|\textbf{r}'(t)|} \; dt = \int_{t_a}^{t_b} \textbf{F}(\textbf{r}(t)) \cdot \textcolor{skyblue}{\textbf{r}'(t) \; dt} $$
비슷하게 삼변수 벡터장의 면적분은 다음과 같이 정의된다.
$$ \iint_S \textbf{F} \cdot \textcolor{skyblue}{d\textbf{S}} = \iint_S \textbf{F} \cdot \textcolor{skyblue}{\textbf{n} \; dS} $$
여기서 $\textbf{n}$ 은 곡면의 접평면의 단위 법선벡터이다.
따라서 의미를 해석해보자면,
곡면위의 모든 부분에 대해 해당 위치에서 벡터의 면에 수직방향인 성분들을 합한 것이라고 할 수 있다.
좀 더 쉽게 표현해서, 그 곡면을 통과하는 벡터장의 양 정도로 생각할 수 있다.
참고로 좌변의 $d\textbf{S}$ 의 $\textbf{S}$ 는 벡터이므로 볼드체이고
우변의 $dS$ 는 스칼라라서 볼드체가 아님에 유념하자.
곡면 $S$ 는 다음과 같이 표현되는 벡터함수이고
($dS$ 의 $S$ 가 아니라 적분 구간의 $S$ 이다. 같은 문자로 쓰여있지만 다른 기호라고 생각해야 한다.)
$$ \textbf{r}(u, v) = <x(u, v), \; y(u, v), \; z(u, v)> $$
$dS$ 는 미소 곡면의 면적이므로 다음과 같이 표현된다. (이 글의 매개변수 곡면의 넓이 파트 참조)
$$ \textcolor{skyblue}{dS} = \textcolor{skyblue}{|\textbf{r}_u \times \textbf{r}_v| \; du dv} $$
임의의 매개변수 $(u, v)$ 가 대응시키는 곡면 위 점에서의 접평면의 법선 벡터가 $\textbf{r}_u \times \textbf{r}_v$ 이므로
여기에 이 것의 크기인 $|\textbf{r}_u \times \textbf{r}_v|$ 로 나누어주면 단위 법선벡터 $\textbf{n}$ 이 될 것이다.
$$ \textcolor{skyblue}{\textbf{n}} = \textcolor{skyblue}{\dfrac{\textbf{r}_u \times \textbf{r}_v}{|\textbf{r}_u \times \textbf{r}_v|}} $$
따라서 $\displaystyle \iint_S \textbf{F} \cdot \textbf{n} \; dS $ 를 다음과 같이 매개변수 $u, v$ 에 대한 이중적분으로 표현할 수 있다.
$$ \iint_S \textbf{F} \cdot \textcolor{skyblue}{\textbf{n} \; dS} = \iint_D \textbf{F}(\textbf{r}(u, v)) \cdot \dfrac{\textbf{r}_u \times \textbf{r}_v}{ \cancel{| \textbf{r}_u \times \textbf{r}_v |} } \cancel{|\textbf{r}_u \times \textbf{r}_v|} \; du dv = \iint_D \textbf{F}(\textbf{r}(u, v)) \cdot \textcolor{skyblue}{(\textbf{r}_u \times \textbf{r}_v) \; dudv} $$
참고로 벡터장이 힘을 나타내는 함수일 때 이 것의 선적분은 일을 나타낸다는 물리학적 의미가 있었듯이
벡터장의 면적분에도 유량(Flux) 이라는 물리학적 의미가 있다.
예제 1
구면 $x^2 + y^2 + z^2 = 1$ 을 통과하는 벡터장 $\textbf{F} = <z, \; y, \;x>$ 의 유량을 구하라.
우선 곡면을 매개 변수로 나타내야 한다.
곡면이 반지름이 $1$ 인 구면이므로 $\rho = 1$ 으로 고정시킨 구면좌표계를 이용하면 될 것이다.
그러면 $x, y, z$ 성분은 다음과 같이 표현되고
$$ \begin{cases} x = \sin{\phi}\cos{\theta} \\ y = \sin{\phi}\sin{\theta} \\ z = \cos{\phi} \end{cases} $$
모든 성분이 두 개의 독립변수 $\phi, \theta$ 에만 의존하므로 다음과 같이 매개곡면을 표현할 수 있다.
$$ \textbf{r}(\phi, \theta) = <\sin{\phi}\cos{\theta}, \; \sin{\phi}\sin{\theta}, \; \cos{\phi}>, \quad 0 \le \phi \le \pi, \quad 0 \le \theta \le 2\pi$$
각 변수 $\phi, \theta$ 에 대한 편미분은 다음과 같고
$$ \begin{cases} \textbf{r}_{\phi} = <\cos{\phi}\cos{\theta}, \; \cos{\phi}\sin{\theta}, \; -\sin{\phi}> \\ \textbf{r}_{\theta} = <-\sin{\phi}\sin{\theta}, \; \sin{\phi}\cos{\theta}, \; 0 > \end{cases} $$
이 둘을 외적하면 다음과 같다.
$$ \textcolor{skyblue}{\textbf{r}_{\phi} \times \textbf{r}_{\theta}} = \textcolor{skyblue}{<\sin^2{\phi}\cos{\theta}, \sin^2{\phi}\sin{\theta}, \sin{\phi}\cos{\phi}>} $$
그리고 $\textbf{F}(\textbf{r}(\phi, \theta))$ 는 다음과 같다.
$$ \textcolor{orange}{\textbf{F}( \textbf{r} (\phi, \theta) )} = \textcolor{orange}{<\cos{\phi}, \; \sin{\phi}\sin{\theta}, \; \sin{\phi}\cos{\theta}>} $$
벡터장의 유량은 이 벡터장의 면적분이므로 다음과 같이 계산된다.
$$ \begin{align} \text{Flux} = \iint_S \textbf{F} \cdot d\textbf{S} = &\iint_D \textcolor{orange}{\textbf{F}(\textbf{r}(\phi, \theta))} \cdot \textcolor{skyblue}{(\textbf{r}_{\phi} \times \textbf{r}_{\theta})} \; d\phi d\theta \\ = &\int_{0}^{2\pi} \int_{0}^{\pi} 2\sin^2{\phi}\cos{\phi}\cos{\theta} + \sin^3{\phi}\sin^2{\theta} \; d\phi d\theta \\ = &2\left[\int_{0}^{\pi} \sin^2{\phi}\cos{\phi} \; d\phi \right] \cdot \cancelto{0}{\left[ \int_{0}^{2\pi} \cos{\theta} \; d\theta \right]} + \left[ \int_{0}^{\pi} \sin^3{\phi} \; d\phi \right] \cdot \left[ \int_{0}^{2\pi} \sin^2{\theta} \; d\theta \right] \\ = &\left[\int_{0}^{\pi} \sin^3{\phi} \; d\phi \right] \cdot \left[ \int_{0}^{2\pi} \sin^2{\theta} \; d\theta \right] \\ = &\textcolor{royalblue}{\dfrac{4}{3}\pi} \end{align} $$
($\displaystyle \int \sin^3{\theta} \; d\theta $ 는 $\sin^3{\theta} = \sin{\theta}(1 - \cos^2{\theta})$ 를 이용하면 계산할 수 있다.)
예제 2
전자기학에서 가우스 법칙(Gauss's Law)은 다음과 같다.
$$ Q = \epsilon_0 \iint_S \textbf{E} \cdot d\textbf{S} $$
여기서 $S$ 는 폐곡면이며 $Q$ 는 곡면 내부의 총 전하량을 얘기하고
$\textbf{E}$ 는 전기장이며 $\epsilon_0$ 은 자유공간에서의 유전율을 의미하는 상수이다.
이 법칙은 폐곡면 $S$ 안에 존재하는 총 전하량 $Q$ 는
곡면을 지나는 전기장의 합에 유전율을 곱한것과 같음을 의미한다.
전기장이 다음과 같이 주어져 있을 때
$$ \textbf{E} = <x, \; y, \; 2z> $$
가우스 법칙을 이용하여
반 구 모양의 영역 $x^2 + y^2 + z^2 \le a^2, \quad z \geq 0$ 안에 있는 총 전하량을 구하라.
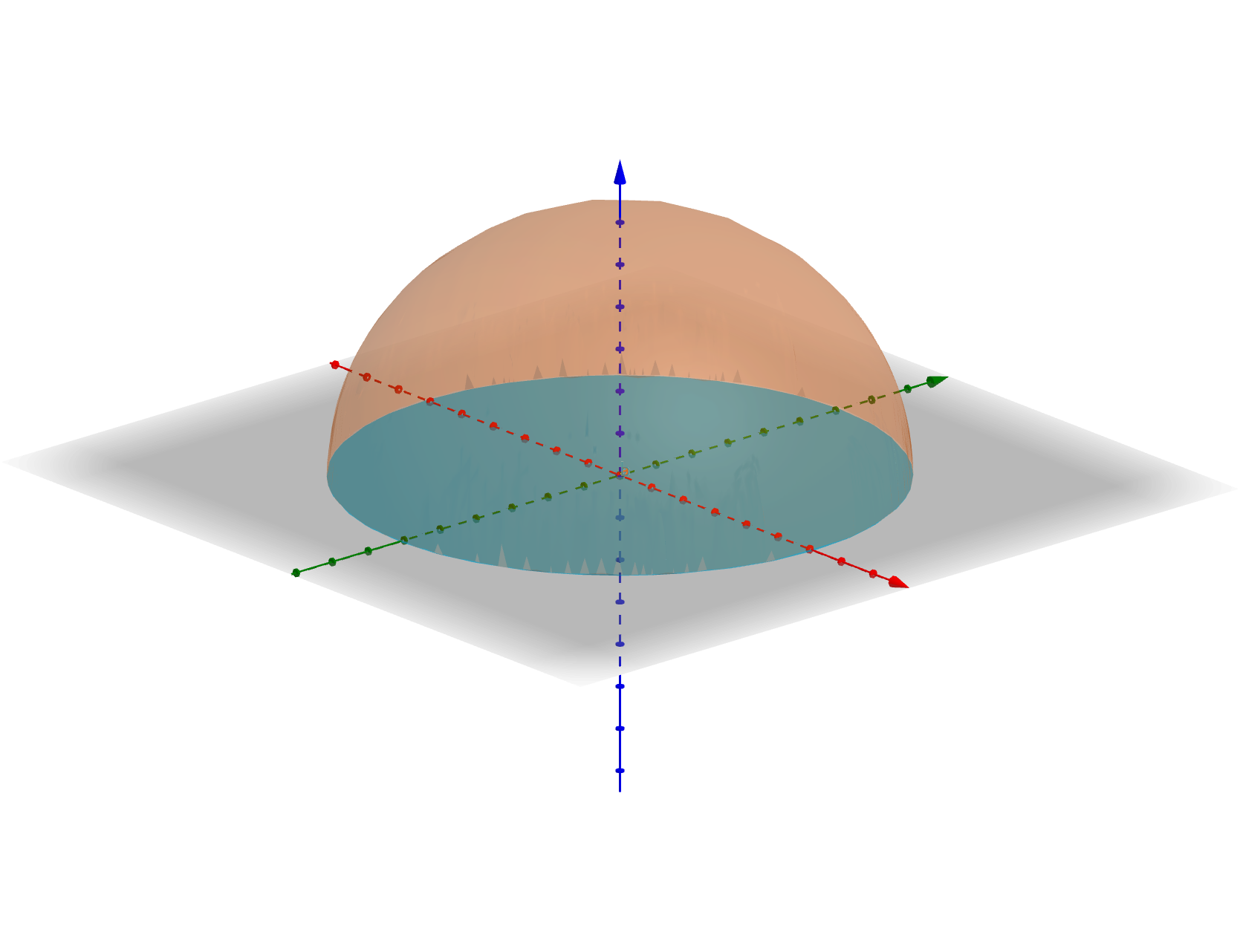
반 구 영역의 경계를 다음과 같이 두 곡면으로 나누어 생각하자.
1. $S_1$ : 돔 형태의 덮개 곡면
2. $S_2$ : 평평한 원형의 밑면
1. 돔 형태의 덮개 곡면
곡면이 구의 형태를 하고 있으므로 구면 좌표계를 도입하면 편할 것이다.
반지름이 $\rho = a$ 로 고정되어 있으므로 $\phi, \theta$ 의 오직 두 변수만이 남는다.
따라서 $S_1$ 를 매개곡면으로 표현하면 다음과 같다.
$$ S_1 : \textbf{r}(\phi, \theta) = <a\sin{\phi}\cos{\theta}, \; a\sin{\phi}\sin{\theta}, \; a\cos{\phi}>, \quad 0 \le \phi \le \dfrac{\pi}{2}, \quad 0 \le \theta \le 2\pi $$
구가 아니라 반구였으므로 $\phi \le \dfrac{\pi}{2}$ 라고 해야하는데, 여기서 실수하지 않아야 한다.
이 것의 $\phi, \theta$ 에 대한 편미분은 다음과 같고
$$ \begin{cases} \textbf{r}_{\phi} = <a\cos{\phi}\cos{\theta}, \; a\cos{\phi}\sin{\theta}, \; -a\sin{\phi}> \\ \textbf{r}_{\theta} = <-a\sin{\phi}\sin{\theta}, \; a\sin{\phi}\cos{\theta}, 0> \end{cases} $$
둘을 외적하면 다음과 같다.
$$ \textcolor{skyblue}{\textbf{r}_{\phi} \times \textbf{r}_{\theta}} = \textcolor{skyblue}{<a^2\sin^2{\phi}\cos{\theta}, \; a^2\sin{\phi}\sin{\theta}, a^2\sin{\phi}\cos{\phi}>} $$
그리고 $\textbf{E}(\textbf{r}(\phi, \theta))$ 는 다음과 같다.
$$ \textcolor{orange}{\textbf{E}(\textbf{r}(\phi, \theta))} = \textcolor{orange}{<a\sin{\phi}\cos{\theta}, \; a\sin{\phi}\sin{\theta}, \; 2a\cos{\phi}>} $$
이를 대입하면 $\displaystyle \iint_{S_1} \textbf{E} \cdot d\textbf{S}$ 는 다음과 같이 계산된다.
$$ \begin{align} \textcolor{royalblue}{\iint_{S_1} \textbf{E} \cdot d\textbf{S}} = &\iint_{D} \textcolor{orange}{\textbf{E}(\textbf{r}(\phi, \theta))} \cdot \textcolor{skyblue}{(\textbf{r}_{\phi} \times \textbf{r}_{\theta})} \; d\phi d\theta \\ = &\int_{0}^{2\pi} \int_{0}^{\frac{\pi}{2}} a^3\sin^3{\phi}\cos^2{\theta} + a^3\sin^3{\phi}\sin^2{\theta} + 2a^3\sin{\phi}\cos^2{\phi} \; d\phi d\theta \\ = &\int_{0}^{2\pi} \int_{0}^{\frac{\pi}{2}} a^3\sin{\phi}(1 + \cos^2{\phi}) \; d\phi d\theta \\ = &2\pi a^3 \left[ \int_0^{\frac{\pi}{2}} \sin{\phi} \; d\phi + \int_0^{\frac{\pi}{2}} \sin{\phi}\cos^2{\phi} \; d\phi \right] \\ = &2\pi a^3 \left[ 1 + \int_0^1 t^2 \; dt \right] = \textcolor{royalblue}{\dfrac{8}{3}a^3 \pi} \end{align}$$
2. 평평한 원형의 밑면
곡면이 평평하고 원형이므로 원통 좌표계를 이용하여 다음과 같이 표현해보자.
$$ S_2 : \textbf{r}(r, \theta) = <r\cos{\theta}, \; r\sin{\theta}, \; 0> $$
그러면 $r, \theta$ 의 편미분은 각각 다음과 같고
$$ \begin{cases} \textbf{r}_{r} = <\cos{\theta}, \; \sin{\theta}, \; 0> \\ \textbf{r}_{\theta} = <-r\sin{\theta}, \; r\cos{\theta}, \; 0> \end{cases} $$
둘을 외적하면 다음과 같다.
$$ \textcolor{skyblue}{\textbf{r}_r \times \textbf{r}_{\theta}} = \textcolor{skyblue}{<0, \; 0, \; r>} $$
그리고 $\textbf{E}(\textbf{r}(r, \theta))$ 는 다음과 같은데
$$ \textcolor{orange}{\textbf{E}(\textbf{r}(r, \theta))} = \textcolor{orange}{<r\cos{\theta}, \; r\sin{\theta}, \; 0>} $$
이 둘을 내적하면 $0$ 이 되어버려서 적분을 계산할 필요도 없이 $\displaystyle \textcolor{royalblue}{\iint_{S_2} \textbf{E} \cdot d\textbf{S} = 0}$ 이다.
두 결과를 더하면 다음과 같고
$$ \begin{align} \iint_S \textbf{E} \cdot d\textbf{S} = &\iint_{S_1} \textbf{E} \cdot d\textbf{S} + \iint_{S_2} \textbf{E} \cdot d\textbf{S} \\ = &\dfrac{8}{3}a^3\pi + 0 \\ = &\dfrac{8}{3}a^3 \pi \end{align} $$
여기에 유전상수 $\epsilon_0$ 을 곱해주면 가우스 법칙에 의해 총 전하량을 계산할 수 있다.
$$ Q = \epsilon_0 \iint_S \textbf{E} \cdot d\textbf{S} = \dfrac{8}{3}a^3\pi \epsilon_0 $$
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 발산 정리(Divergence Theorem) (0) | 2023.10.23 |
|---|---|
| 스토크스 정리(Stokes' Theorem) (0) | 2023.10.20 |
| 스칼라 함수의 면적분(Surface Integrals on Scalar Functions) (0) | 2023.10.18 |
| 매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas) (0) | 2023.10.17 |
| 그린 정리와 그 의미(Green's Theorem) (0) | 2023.10.14 |