앞서 그린 정리에서 발산에 관한 그린 정리에 대해 소개한 바가 있다.
발산 정리(2차원)
$$ \oint_C \textbf{F} \cdot \textbf{n} \; ds = \iint_D \nabla \cdot \textbf{F} \; dA $$
좌변은 폐곡선 상에서의 벡터장의 발산 정도를 나타내고
우변은 폐곡선이 만드는 영역위의 모든 점에서 벡터장의 발산을 합한 값을 나타내므로
"어떤 영역(평면)에서의 벡터장의 발산은 그 경계에서의 발산이랑 같다" 를 의미한다고 했었다.
이번에 소개할 발산정리는 위 정리를 3차원으로 확장시켜서 같은 논리로
"어떤 영역(공간)에서의 벡터장의 발산은 그 경계면에서의 발산이랑 같다"
라는 의미를 갖는 정리이고 식으로 다음과 같이 표현한다.
발산 정리(3차원)
공간속에 유계이고 닫힌 영역 $E$ 가 있고,
이 영역의 경계를 $S$ 라고 하는데, 면의 방향은 바깥을 향하는 방향이라고 하자.
벡터장 $\textbf{F}$ 가 $E$ 를 포함하는 열린 영역에서 각 성분이 연속인 편도함수를 가지면 다음이 성립한다.
$$ \iint_S \textbf{F} \cdot \textbf{n} \; dS = \iiint_E \nabla \cdot \textbf{F} \; dV $$
이 때 좌변의 면적분은 간단히 $\displaystyle \iint_S \textbf{F} \cdot d\textbf{S}$ 라고 써도 되는데
2차원에서 발산정리 식이랑 통일감을 주기 위해 $d\textbf{S}$ 대신 굳이 $\textbf{n} \; dS$ 로 썼다.
참고로 스튜어트 책에 수록된 발산 정리의 증명은 완벽한 증명이 아니다.
스튜어트에는 "simple solid region" 인 $E$ 에 대해서 발산 정리를 서술해 놓았고
이러한 영역에 대해서만 증명을 했는데,
사실 이 보다는 좀 더 확장된 영역에서도 발산정리는 성립하므로
simple solid region이 아닌 영역에 대해서도 증명을 써주었어야 완벽한 증명이다.
자세한건 미적분학 수준에서 다루기 어려우므로 넘어가자.
예제 1
벡터장이 다음과 같이 주어져 있을 때
$$ \textbf{F} = <z, \; y, \; x> $$
구면 $S : x^2 + y^2 + z^2 = 1$ 에서의 유량(Flux) 를 계산하라.
유량은 주어진 벡터장의 곡면 위에서의 면적분을 얘기하므로 다음 식을 구하는 것이다.
$$ \iint_S \textbf{F} \cdot d\textbf{S} $$
발산 정리를 알기 전에는 이를 계산하기 위해
곡면을 매개변수화 하고 또 이를 편미분하고 외적해주어 면의 방향을 구하고
매개변수 함수를 대입해가며 복잡하게 면적분을 직접 계산했어야 했다.
하지만 이 곡면은 폐곡면이므로 발산 정리를 이용할 수 있다.
발산정리에 의하면 다음과 같으므로
$$ \iint_S \textbf{F} \cdot d\textbf{S} = \iiint_E \nabla \cdot \textbf{F} \; dV $$
$\displaystyle \iint_S \textbf{F} \cdot d\textbf{S} $ 대신 $\displaystyle \iiint_E \nabla \cdot \textbf{F} \; dV$ 를 계산해도 된다.
그리고
$$ \nabla \cdot \textbf{F} = \dfrac{\partial z}{\partial x} + \dfrac{\partial y}{\partial y} + \dfrac{\partial x}{\partial z} = 1$$
이므로 이를 대입하면 다음과 같이 계산 된다.
$$ \iiint_E \nabla \cdot \textbf{F} \; dV = \iiint_E 1 \; dV = \textcolor{orange}{\text{E 의 부피}} = \textcolor{royalblue}{\dfrac{4}{3}\pi} $$
따라서 주어진 벡터장$\textbf{F}$ 의 $S$ 에서의 유량은 다음과 같다.
$$ \iint_S \textbf{F} \cdot d\textbf{S} = \dfrac{4}{3}\pi $$
예제 2
벡터장 $\textbf{F}$ 가 다음과 같이 주어져 있고
$$ \textbf{F} = <xy, \; y^2 + e^{xz^2}, \; \sin{(xy)}> $$
영역 $E$ 는 포물면 $z = 1- x^2$ 과 세 평면 $z = 0$, $y = 0$, $y + z = 2$ 로 유계된 영역이며
이 경계를 $S$ 라고 할 때, 다음을 계산하라.
$$ \iint_S \textbf{F} \cdot d\textbf{S} $$
주어진 영역을 그려보면 다음과 같다.
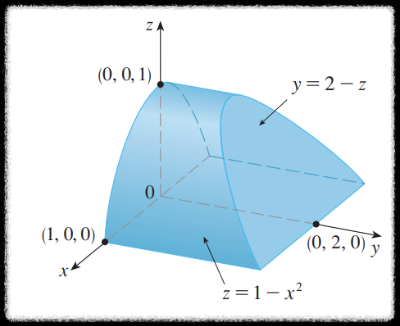
이 역시 발산 정리를 알기 전에는 네 곡면으로 나누어 각각에 대해 복잡한 면적분을 계산해주어야 했다.
하지만 $S$ 가 폐곡면이므로 발산 정리를 이용할 수 있는데
심지어 $\nabla \cdot \textbf{F}$ 를 계산해보면
$$ \textcolor{orange}{\nabla \cdot \textbf{F}} = \dfrac{\partial (xy)}{\partial x} + \dfrac{\partial (y^2 + e^{xz^2})}{\partial y} + \dfrac{\partial (\sin{(xy)})}{\partial z} = \textcolor{orange}{3y} $$
으로 단순한 식이 나오기 때문에, 발산정리를 이용하면 적분이 훨씬 간단해질 것이다.
발산정리를 이용할 것이므로 $\nabla \cdot \textbf{F}$ 의 주어진 영역 $E$ 에서의 삼중적분을 계산해야 한다.
그림을 살펴보면 적분을 $yzx$ 순서로 하면 구간을 분리할 필요 없어서 제일 편해보인다.
이 순서를 따르면 주어진 영역 $E$ 는 다음과 같이 표현되고
$$ E : \begin{cases} 0 \le y \le 2-z \\ 0 \le z \le 1- x^2 \\ -1 \le x \le 1 \end{cases} $$
발산 정리와 이 정보를 이용하여 계산해보면 $\displaystyle \iint_S \textbf{F} \cdot d\textbf{S}$ 는 다음과 같다.
$$ \begin{align} \textcolor{royalblue}{\iint_S \textbf{F} \cdot d\textbf{S}} = &\iiint_E \textcolor{orange}{\nabla \cdot \textbf{F}} \; dV \\ = &\iiint_E \textcolor{orange}{3y} \; dV \\ = &\int_{-1}^{1} \int_{0}^{1-x^2} \int_{0}^{2-z} 3y \; dy\;dz\;dx = \textcolor{royalblue}{\dfrac{184}{35}} \end{align} $$
그린 정리에서 그린 정리를 응용하면 가운데 구멍이 있는 영역에 대해서도 적용할 수 있다고 했었다.
비슷하게 발산 정리의 경우에도 영역 내부에 빈 공간이 있더라도 정리를 적용할 수 있는 방법이 있다.
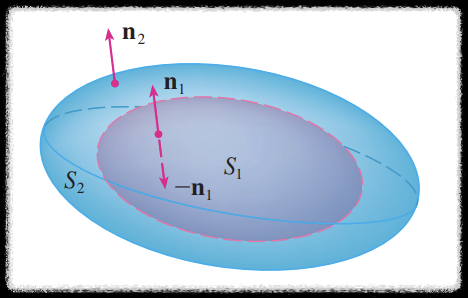
위 그림과 같이 큰 영역(푸른 색) 안에 빈 공간(붉은 색)이 있다고 하자.
그러면 이 영역은 바깥 경계면 $S_2$ 과 내부 경계면 $S_1$ 으로 둘러싸여 있다고 할 수 있다. ($S = S_1 \cup S_2$)
$S_1$, $S_2$ 의 방향 $\textbf{n}_1$, $\textbf{n}_2$ 모두 바깥을 향한다고 정하자.
발산 정리를 이용하기 위해서는 $S$ 의 방향 $\textcolor{skyblue}{\textbf{n}}$ 을 바깥을 향하게 해야하므로
$S_1$ 에서는 $\textcolor{skyblue}{\textbf{n}}$ 이 내부 방향인 $-\textbf{n}_1$
$S_2$ 에서는 $\textcolor{skyblue}{\textbf{n}}$ 이 외부 방향인 $\textbf{n}_2$
라고 정한다.
이제 발산 정리를 이용하면 다음과 같다.
$$ \begin{align} \iiint_E \nabla \cdot \textbf{F} \; dV = &\iint_S \textbf{F} \cdot \textcolor{skyblue}{\textbf{n}} \; dS \\ = &\iint_{S_1} \textbf{F} \cdot (-\textbf{n}_1) \; dS + \iint_{S_2} \textbf{F} \cdot (\textbf{n}_2) \; dS \\ = &-\iint_{S_1} \textbf{F} \cdot d\textbf{S} + \iint_{S_2} \textbf{F} \cdot d\textbf{S} \end{align} $$
정리하면, 내부에 동공을 가진 영역에서 발산 정리를 적용할 땐
바깥 껍질에서의 면적분 - 안쪽 껍질에서의 면적분
을 계산하면 된다는 것이다.
예제 3
원점에 전하 $Q$ 가 놓여있을 때, 이 점전하가 만드는 전기장은
거리 제곱에 반비례 하며 원점으로부터 뻗어나가는 방향을 가지므로
임의의 위치 $\textbf{x} = <x, \; y, \; z>$ 에서의 전기장을 다음과 같이 적을 수 있다.
$$ \textcolor{orange}{\textbf{E}(\textbf{x})} = \dfrac{\epsilon Q}{|\textbf{x}|^2} \dfrac{\textbf{x}}{|\textbf{x}|} = \textcolor{orange}{\dfrac{\epsilon Q}{|\textbf{x}|^3}\textbf{x}} $$
여기서 $\epsilon$ 은 쿨롱 상수이고 $Q$ 는 전하량을 의미한다.
원점을 내부에 포함하는 임의의 폐곡면 $S_2$ 에 대해 다음이 성립함을 보여라
$$ \iint_{S_2} \textbf{E} \cdot d\textbf{S} = 4\pi \epsilon Q $$
$S_2$ 가 식으로 주어져 있지 않고 임의의 곡면으로 주어져 있으므로 $\displaystyle \iint_{S_2} \textbf{E} \cdot d\textbf{S}$ 는 바로 계산하기 힘들다.
발산 정리를 이용하려고 해도 $\textbf{E}$ 가 원점에서 분모가 $0$ 이 되어 정의되지 않기 때문에
바로 발산 정리를 이용할 수도 없다.
하지만 위에서 설명한 방법대로
$S_2$ 내부에 원점을 둘러싸는 곡면 $S_1$ 을 만들고 $S_1$ 과 $S_2$ 사이에 존재하는 영역을 $D$ 라고 하면
$D$ 에서는 원점이 포함되어 있지 않기 때문에 발산 정리를 이용해볼 수 있다.
그러면 발산 정리의 응용에 의해 다음이 성립한다.
$$ \iiint_D \nabla \cdot \textbf{E} \; dV = \iint_{S_2} \textbf{E} \cdot d\textbf{S} - \iint_{S_1} \textbf{E} \cdot d\textbf{S} \tag{1}$$
$\nabla \cdot \textbf{E}$ 를 계산해보면 다음과 같이 $0$ 이 나오므로
$$ \begin{align} \textcolor{skyblue}{\nabla} \cdot \textcolor{orange}{\textbf{E}} = &\textcolor{skyblue}{<\dfrac{\partial }{\partial x}, \; \dfrac{\partial}{\partial y}, \; \dfrac{\partial}{\partial z}>} \cdot \; \textcolor{orange}{\epsilon Q \dfrac{<x, \; y, \; z>}{(x^2 + y^2 + z^2)^{\frac{3}{2}}}} \\ = &\epsilon Q \left[ \dfrac{y^2 + z^2 - 2x^2}{(x^2 + y^2 + z^2)^{\frac{5}{2}}} + \dfrac{x^2 + z^2 - 2y^2}{(x^2 + y^2 + z^2)^{\frac{5}{2}}} + \dfrac{x^2 + y^2 - 2z^2}{(x^2 + y^2 + z^2)^{\frac{5}{2}}} \right] \\ = &\epsilon Q \cdot 0 = \textcolor{royalblue}{0} \end{align} $$
식 (1) 의 좌변은 $0$ 이고 다음 결론을 얻는다.
$$ \iint_{S_2} \textbf{E} \cdot d\textbf{S} = \iint_{S_1} \textbf{E} \cdot d\textbf{S} $$
이는 해석하자면 $S_1$ 에서의 면적분과 $S_2$ 에서의 면적분이 같다는 의미인데
$S_1$, $S_2$ 모두 임의로 설정한 곡면이였으므로
원점을 내부에 포함하기만 한다면 아무런 폐곡면에 대해 면적분을 계산해도 값이 같다는 결론이 나온다.
$S_1$ 을 계산하기 쉽도록 반지름이 $a$ 인 구의 표면이라고 하자.
그러면 $S_1$ 는 벡터방정식으로 $|\textbf{x}| = a$ 라고 쓸 수 있다.
(단 $a$ 는 반지름이 충분히 작아서 곡면 $S_2$ 안에 충분히 포함된다고 한다.)
우리가 계산해야 하는 것은 $\displaystyle \iint_{S_1} \textbf{E} \cdot d\textbf{S} = \iint_{S_1} \textcolor{orange}{\textbf{E} \cdot \textbf{n}} \; dS$ 인데
$\textbf{x}$ 에서의 곡면 $S_1$ 의 단위법선벡터가 $\textbf{n} = \dfrac{\textbf{x}}{|\textbf{x}|}$ 이므로
$$ \textcolor{orange}{\textbf{E} \cdot \textbf{n}} = \dfrac{\epsilon Q}{|\textbf{x}|^3}\textbf{x} \cdot \dfrac{\textbf{x}}{|\textbf{x}|} = \dfrac{\epsilon Q}{|\textbf{x}|^4}|\textbf{x}|^2 = \dfrac{\epsilon Q}{|\textbf{x}|^2} = \textcolor{orange}{\dfrac{\epsilon Q}{a^2}} $$
따라서 다음과 같다.
$$ \begin{align} \textcolor{royalblue}{\iint_{S_2} \textbf{E} \cdot d\textbf{S}} = &\iint_{S_1} \textbf{E} \cdot \textbf{n} \; dS \\ = &\dfrac{\epsilon Q}{a^2} \textcolor{skyblue}{\iint_{S_1} \; dS} = \dfrac{\epsilon Q}{a^2} \cdot \textcolor{skyblue}{S_1 \text{ 의 겉넓이}} = \dfrac{\epsilon Q}{a^2}\textcolor{skyblue}{(4\pi a^2)} = \textcolor{royalblue}{4\pi \epsilon Q} \end{align} $$
참고로 쿨롱 상수는 $\epsilon = \dfrac{1}{4 \pi \epsilon_0}$ 로 정의가 되어있고 ($\epsilon_0$ 은 진공에서의 유전율상수)
이를 결과에 대입하면
원점(전하가 존재하는 곳)을 둘러싸는 임의의 폐곡면 $S$ 에 대해 다음이 성립한다.
$$ \epsilon_0 \iint_{S} \textbf{E} \cdot d\textbf{S} = Q $$
그리고 이는 전기장의 원천은 전하라는 의미를 갖는 가우스 법칙이다.
이로써 스튜어트미적분학의 모든 단원이 끝났다.
연습문제를 통해 마무리하자.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| [연습 문제] 선적분, 면적분, 그린 정리, 스토크스 정리, 발산 정리 (0) | 2023.10.24 |
|---|---|
| 스토크스 정리(Stokes' Theorem) (0) | 2023.10.20 |
| 벡터 함수의 면적분(Surface Integrals on Vector Fields) (0) | 2023.10.19 |
| 스칼라 함수의 면적분(Surface Integrals on Scalar Functions) (0) | 2023.10.18 |
| 매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas) (0) | 2023.10.17 |