앞서 그린 정리를 소개하면서 그린 정리는 스토크스 정리의 특수한 경우라고 언급했었다.
이제 그 스토크스 정리에 대해 알아보자.
정리를 소개하기 앞서 닫힌 곡면에서 곡면의 방향과
곡면의 경계선의 진행방향의 관계에 대해 다음과 같이 먼저 약속을 하고 가자.
어떤 방향이 있는 유향 곡면 $S$ 가 있고 이 곡면의 경계를 $C$ 라고 하자.
곡면 $S$ 는 앞 뒤의 두 방향이 존재하는데, 둘 중 한 방향을 정해 단위벡터로 $\textbf{n}$ 이라 하자.
그리고 $\textbf{n}$ 이 향하는 방향 위에서 곡면을 바라보았을 때
$C$ 의 진행방향이 반시계 방향이 되도록 정한다.

스토크스 정리(Stokes' Theorem)
$S$ 가 닫혀있는 조각적으로 부드러운 단순곡선 $C$ 를 경계로 하는
조각적으로 부드러운 유향곡면이라고 하자.
그리고 $\textbf{F}$ 가 곡면 $S$ 를 포함하는 $\mathbb{R}^3$ 상의 열린 공간에서
각 성분이 연속인 편도함수를 가지는 벡터장이라고 하면 다음이 성립한다.
$$ \int_C \textbf{F} \cdot d\textbf{r} = \iint_S (\nabla \times \textbf{F}) \cdot d\textbf{S} $$
$\nabla \times \textbf{F} = \text{curl }\textbf{F}$ 이므로 다음과 같이 쓸 수도 있다.
$$ \int_C \textbf{F} \cdot d\textbf{r} = \iint_S \text{curl }\textbf{F} \cdot d\textbf{S} $$
한편 좌변은 선적분이고 우변은 면적분이므로 다음과 같이 쓸 수도 있다.
$$ \int_C \textbf{F} \cdot \textbf{T} \; ds = \iint_S (\nabla \times \textbf{F}) \cdot \textbf{n} \; dS $$
좌변은 곡선을 따라가는 방향의 벡터장 $\textbf{F}$ 의 성분들의 합을 의미하고
우변은 곡면 위의 모든 점에 대해 그 점에서 법선벡터 $\textbf{n}$ 을 회전 축으로 하는 $\textbf{F}$ 의 회전 (= $\nabla \times \textbf{F}$) 의 합을 의미한다.
대충 얘기하면, 곡면 경계에서의 벡터장 $\textbf{F}$ 의 회전 정도(좌변)은
곡면위의 각 점에서 회전 정도를 다 더한 것(우변)과 같다라고 할 수 있겠다.
이번에 소개한 스토크스 정리가
그린 정리, 선적분의 기본정리, 미적분학의 기본정리랑 모두 유사하다는 것을 눈치 챘는가?
우선 미적분학의 기본정리는 다음과 같다.
$$ \int_a^b \dfrac{d}{dx} F(x) \; dx = F(b) - F(a) $$
1. 좌변과 우변의 적분 갯수가 하나 차이나고
2. 적분 갯수가 많은 쪽(좌변)에는 미분과 관련된 식($\dfrac{d}{dx}$)이 있으며
3. 적분 갯수가 적은 쪽(우변)에는 적분의 경계와 관련된 식이 있다.
그리고 미적분학의 기본정리의 매개변수화 버전이 선적분의 기본정리이며 다음과 같았다.
$$ \int_C \nabla f \cdot d\textbf{r} = f(\textbf{r}(b)) - f(\textbf{r}(a)) $$
이것 역시
1. 좌변과 우변의 적분 갯수가 하나 차이나고
2. 적분 갯수가 많은 쪽에는 미분과 관련된 식 ($\nabla$) 이 있으며
3. 적분 갯수가 적은 쪽에는 적분의 경계와 관련된 식이 있다.
그린 정리는 다음과 같았는데
$$ \iint_D (\nabla \times \textbf{F}) \cdot \textbf{k} \; dA = \int_C \textbf{F} \cdot d\textbf{r} $$
이것 또한 역시
1. 좌변과 우변의 적분 갯수가 하나 차이나고
2. 적분 갯수가 많은 쪽에는 미분과 관련된 식 ($\nabla$) 이 있으며
3. 적분 갯수가 적은 쪽에는 적분의 경계 (곡선 $C$ 가 영역 $D$ 의 경계) 와 관련된 식이 있다.
그런데 이번에 소개한 스토크스 정리 또한 그렇다.
$$ \iint_S (\nabla \times \textbf{F}) \cdot d\textbf{S} = \int_C \textbf{F} \cdot d\textbf{r} $$
1. 좌변과 우변의 적분 갯수가 하나 차이나고
2. 적분 갯수가 많은 쪽에는 미분과 관련된 식 ($\nabla$) 이 있으며
3. 적분 갯수가 적은 쪽에는 적분의 경계 (곡선 $C$ 가 곡면 $S$ 의 경계) 와 관련된 식이 있다.
심지어 선적분의 기본정리가 미적분학의 기본정리의 매개변수 버전이였듯이
스토크스 정리는 그린정리의 매개변수 버전이라는 점도 발견할 수 있다!
따라서 그린 정리를 이중적분의 기본정리,
스토크스 정리를 면적분의 기본정리(?) 쯤으로 생각할 수도 있다. (공식 용어가 아니다)
스토크스 정리의 증명 역시 그린 정리처럼 미적분학 수준에서는 하기 힘들다.
실제 증명은 수학과 전공 과목인 미분기하학에서 이루어지는데,
임의 차원의 미분다양체에 대한 일반화된 스토크스 정리를 먼저 증명한 후
그린 정리나 스토크스 정리나 미적분학의 기본정리등은 일반화된 스토크스 정리의 특수한 경우라고 하여 증명한다.
참고로 스튜어트 책에 나와있는 증명은
특수한 형태의 곡면인 경우에 대해서만 증명한 것이고 일반적인 경우를 증명한 것이 아니므로
한 번만 읽고 넘어가고 그냥 스토크스 정리의 의미만 파악한 후 문제나 풀어보는게 낫다.
예제 1
곡선 $C$ 가 평면 $y + z = 2$ 와 원통 $x^2 + y^2 = 1$ 이 만나서 생기는 곡선이고
위에서 바라보았을 때 반시계 방향을 갖는다고 하자.
벡터장이 $\textbf{F} = <-y^2, \; x, \; z^2>$ 으로 주어져 있을 때 다음 선적분을 계산하라.
$$ \int_C \textbf{F} \cdot d\textbf{r} $$
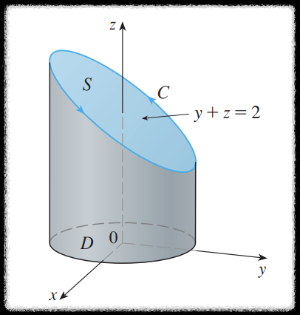
곡선 $C$ 는 위 그림과 같이 타원형의 폐곡선인데
이 곡선을 경계로 갖는 임의의 부드러운 곡면 $S$ 를 상정하면 스토크스 정리를 이용할 수 있다.
경계가 $C$ 이고 부드럽기만 하면 아무런 곡면 $S$ 를 만들어도 상관없지만
계산의 편의를 위해서는 간단한 곡면을 상정하는 것이 좋을 것이다.
$S$ 를 $y+z = 2$ 로 두자.
이를 변형하면 $z = 2 - y$ 이고 $x, y$ 를 두 매개변수라고 하면
$x$ 성분은 그냥 $x$
$y$ 성분도 그냥 $y$
$z$ 성분은 $2- y$
이므로 곡면을 매개변수 $x ,y$ 에 대한 벡터함수로 다음과 같이 표현할 수 있을 것이다.
$$ S : \textbf{r}(x, y) = <x, \; y, \; 2-y> $$
이 곡면의 $x, y$ 에 대한 편도함수는 다음과 같고
$$ \begin{cases} \textbf{r}_x = <1, \; 0, \; 0> \\ \textbf{r}_y = <0, \; 1, \; -1> \end{cases} $$
둘을 외적하면 다음과 같다.
$$ \textcolor{skyblue}{\textbf{r}_x \times \textbf{r}_y} = \textcolor{skyblue}{ <0, \; 1, \; 1> }$$
한편 $\nabla \times \textbf{F}$ 는 다음과 같다.
$$ \textcolor{orange}{\nabla \times \textbf{F}} = \begin{vmatrix} \textbf{i} & \textbf{j} & \textbf{k} \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\ -y^2 & x & z^2 \end{vmatrix} = \textcolor{orange}{<0, \; 0, \; 1 + 2y>} $$
이제 스토크스 정리를 이용하면 다음과 같다.
$$ \begin{align} \textcolor{royalblue}{\int_C \textbf{F} \cdot d\textbf{r}} = &\iint_S \textcolor{orange}{(\nabla \times \textbf{F})} \cdot \textcolor{skyblue}{\textbf{n}} \; dS \\ = &\iint_D \textcolor{orange}{<0, \; 0 , \; 1 + 2y>} \cdot \textcolor{skyblue}{<0, \; 1, \; 1>} \; dA \\ = &\iint_D 1 + 2y \; dA \end{align} $$
이 때 영역 $D$ 는 매개변수인 $x, y$ 들이 놓이는 영역으로 원형 영역인 $x^2 + y^2 \le 1$ 이므로
극좌표계로 변환하여 적분을 계산하면 편할 것이다.
$$ \begin{align} \iint_D 1 + 2y \; dA = &\int_0^{2\pi} \int_0^1 (1 + 2r\sin{\theta})r \; drd\theta \\ = &\int_0^{2\pi} \left[ \dfrac{1}{2}r^2 + \dfrac{2}{3}r^3 \sin{\theta} \right]_0^1 \; d\theta \\ = &\int_0^{2\pi} \dfrac{1}{2} + \dfrac{2}{3}\sin{\theta} \; d\theta = \textcolor{royalblue}{\pi} \end{align} $$
($\sin{\theta}$ 를 $0 \to 2\pi$ 까지 적분한 것은 $0$ 이므로 바로 $\frac{1}{2}$ 에 대해서만 적분해주면 된다.)
$$ \therefore \int_C \textbf{F} \cdot d\textbf{r} = \pi $$
앞서 보존장인지 판단하는 방법중 하나로
$\text{curl }\textbf{F} = \textbf{0}$ 이면 $\textbf{F}$ 는 보존장이라는 정리를 소개했었다.
이 것은 스토크스 정리의 결과인데,
그 어떤 $S$ 에 대해서라도(단, $S$ 의 경계가 단순 곡선이 되야만 한다) $\text{curl }\textbf{F} = \nabla \times \textbf{F} = \textbf{0}$ 이면
$$ \iint_S (\nabla \times \textbf{F}) \cdot \textbf{n} \; dS = \iint_S 0 \; dS = 0$$
이므로 스토크스 정리에 의해 $\displaystyle \int_C \textbf{F} \cdot d\textbf{r} = 0$ 가 된다.
그리고 $S$ 가 임의의 곡면이라고 했으므로 이것의 경계인 $C$ 도 임의의 (단순)곡선이 될 것이고
임의의 폐곡선 $C$ 에 대해 $\displaystyle \int_C \textbf{F} \cdot d\textbf{r} = 0$ 이면 $\textbf{F}$ 는 보존장이다 라는 정리를 이용하면
$\text{curl }\textbf{F} = \textbf{0}$ 이면 $\textbf{F}$ 는 보존장이다가 증명이 된다.
근데 사실 이 것도 증명이 아니긴 하다.
왜냐하면 스토크스 정리는 $C$ 가 조각적으로 단순곡선일때에 대해 서술한 정리이고
위에서 스토크스 정리의 결과로 보인 $\displaystyle \int_C \textbf{F} \cdot d\textbf{r} = 0$ 은
"임의의 곡선 $C$" 에 대해 성립하는게 아닌 "조각적으로 단순곡선인 $C$ 에 대해 성립"하는 것을 보인 것이기 때문이다.
조각적 단순곡선이 아닌 $C$ 에 대해서도 $\displaystyle \int_C \textbf{F} \cdot d\textbf{r} = 0$ 이 성립함을 보여야 완벽한 증명이 된다.
책에서는 단순곡선이 아닌 경우는 단순곡선들로 쪼개서 계산하면 된다고 간략히 언급해놓기는 했는데,
임의의 곡선을 단순곡선들을 연결해서 항상 만들어낼 수 있는지가 먼저 증명이 되어야 하는 부분인데
이에 대한 설명은 없어서 필자도 의문이긴 하다
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| [연습 문제] 선적분, 면적분, 그린 정리, 스토크스 정리, 발산 정리 (0) | 2023.10.24 |
|---|---|
| 발산 정리(Divergence Theorem) (0) | 2023.10.23 |
| 벡터 함수의 면적분(Surface Integrals on Vector Fields) (0) | 2023.10.19 |
| 스칼라 함수의 면적분(Surface Integrals on Scalar Functions) (0) | 2023.10.18 |
| 매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas) (0) | 2023.10.17 |