매개변수 곡면과 그 넓이(Parametric Surfaces and Their Areas)

■ 매개변수 곡면의 정의와 의미

 

앞서 2차원 평면에 놓인 곡선을 매개변수 $t$ 를 이용해 다음과 같이 정의했었다.

$$\mathbf{\text{r}}(t)=<x(t),y(t)>$$

만약 곡선이 3차원 공간에 놓여있다면 $z$ 성분을 추가해주기만 하면 됐었다.

$$\mathbf{\text{r}}(t)=<x(t),y(t),z(t)>$$

 

비슷한 방법으로 3차원 상에 존재하는 매개 곡면을 정의해보자.

이 곡면의 $x,y,z$ 값을 표현하기 위해서는 곡선과는 달리 두 개의 독립 변수가 필요하다.

따라서 매개변수 곡면을 다음과 같이 제시할 수 있다.

$$\mathbf{\text{r}}(u,v)=<x(u,v),y(u,v),z(u,v)>$$

이렇게 표현한 $\mathbf{\text{r}}$ 역시 벡터 함수임을 유념하자.

 

 

곡선의 매개변수 표현에서 $t$ 의 값(정의역)이 어떤 구간으로 표현 되었듯이

곡면의 매개변수 $u,v$ 역시 정의역이 존재하는데,

변수가 두 개이므로 이번엔 정의역이 어떤 구간이 아닌 어떤 영역으로 표현 된다.

 

그리고 곡면의 벡터 함수 $\mathbf{\text{r}}(u,v)$ 는 정의역인 $D$ 영역 안의 한 점 $(u,v)$ 를

삼차원 공간상의 어떤 점 $(x,y,z)$ 에 대응시키는 함수이다.

이 의미를 잘 이해하고 넘어가자.

 

 

 

곡면의 벡터 함수 표현의 한 예시를 살펴보자.

$$\mathbf{\text{r}}(u,v)=<2\cos u,v,2\sin u>$$

이 벡터 함수는 풀어 쓰면

곡면의 $x$ 성분이 $2\cos u$

곡면의 $y$ 성분이 $v$

곡면의 $z$ 성분이 $2\sin u$

라는 의미이다.

 

$x,z$ 값을 살펴보면 $x^2+z^2=4$ 가 성립하는데,

이는 $xz$ 평면과 평행한 평면으로 주어진 곡면을 자르면 반지름이 $2$ 인 원이 됨을 의미한다.

 

그리고 $y=v$ 이므로 $v$ 값이 커짐에 따라 $y$ 값도 커지는데,

이는 곡면의 $xz$ 평면으로의 단면이 $y$ 축을 높이 삼아 쭉 이어진다는 뜻이다.

 

둘을 조합해보면,

아래 그림과 같이 $y$ 축 방향으로 무한히 이어지는 원통형 곡면이란걸 알 수 있다.

 

 

 

 

예제 1


반지름이 $a$ 인 구의 표면을 매개변수 함수로 표현하라

그 전에 구면좌표계에서 $x,y,z$ 의 성분을 다음과 같이 표현했었음을 떠올려 보자.

$$\{\begin{array}{l}x=\rho \sin \varphi \cos \theta \\ y=\rho \sin \varphi \sin \theta \\ z=\rho \cos \varphi \end{array}$$

이 때 $\rho ,\varphi ,\theta$ 가 의미하는 바는 아래 그림과 같다.

 

 

 

우리가 찾고자 하는 것은 구의 표면이므로 $\rho$ 값만 고정시키고 나머지는 변수로 놔두면 될 것이다.

따라서 반지름이 $\rho =a$ 인 구의 $x,y,z$ 성분은 다음과 같다.

$$\{\begin{array}{l}x=a\sin \varphi \cos \theta \\ y=a\sin \varphi \sin \theta \\ z=a\cos \varphi \end{array}$$

그리고 이 관계식은 오직 두 변수 $\varphi ,\theta$ 에만 의존하므로

이 것을 두 독립변수 삼으면 구 표면의 매개변수 방정식을 다음과 같이 쓸 수 있을 것이다.

$$\mathbf{\text{r}}(\varphi ,\theta )=<a\sin \varphi \cos \theta ,a\sin \varphi \sin \theta ,a\cos \varphi >$$

 

 

 

 

 

 

 

 

 

 

참고로 매개 변수 곡면 $\mathbf{\text{r}}(u,v)$ 에서 $u$ 또는 $v$ 둘 중 하나를 고정시키면

그 결과는 곡면이 아닌 곡선이 된다.

 

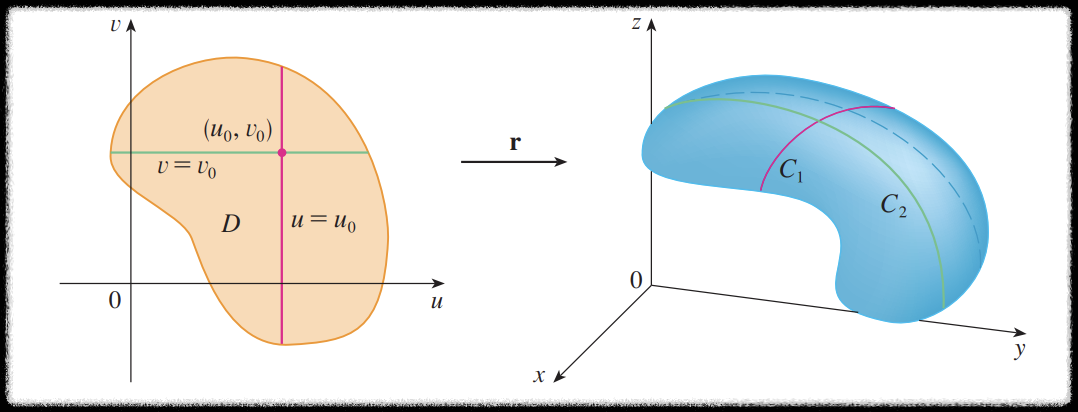
왼쪽의 그림의 초록 선처럼

$v=v_0$ 으로 고정시키면 정의역 영역 안의 초록 색 선 위의 점들이 대응시키는 곡면에서의 점들은

오른쪽 그림에서 곡선 $C_2$ 처럼 곡선으로 나타난다.

마찬가지로 $u=u_0$ 으로 고정시킨 정의역의 붉은 색 선 위의 점들이 대응시키는 곡면에서의 점들은

오른쪽 그림에서 곡선 $C_1$ 처럼 곡선으로 나타난다.

 

고정 값을 일정하게 증가 또는 감소시켜가며 만들어낸 곡선들은

곡면 위에서 격자 형태로 나타나게 될 것인데 이를 격자 곡선이라 부를 것이다.

 

변수 하나를 없애면 곡면이 곡선이 되는 것은 어떻게 생각하면 당연한 것인데

변수가 하나인 매개 변수 벡터 함수는 앞서 배웠 듯 곡면이 아닌 곡선이였기 때문이다.

 

 

 

 

위에서 다룬 원통 예제를 이용하여 이 현상을 확인해보자.

 

$u=0$ 으로 고정했다고 하자. 그러면 $x=2,z=0$ 이다.

그런데 $v$ 에 대한 제약은 없고 $y=v$ 이므로

$u=0$ 일 때 $\mathbf{\text{r}}(u,v)$ 는 다음과 같이 표현되는데, 이는 $y$ 축 방향으로 뻗어나가는 직선을 의미한다.

$$\mathbf{\text{r}}(0,v)=<2,v,0>$$

그리고 이 것은 곡면이 아닌 곡선(직선도 곡선이다)임을 확인할 수 있다

 

 

이번엔 $v=5$ 로 고정했다고 하자. 그러면 $y=5$ 이다

그런데 $u$ 에 대한 제약은 없고 $x=\cos u,z=\sin u$ 이므로

$v=5$ 일 때 $\mathbf{\text{r}}(u,v)$ 는 다음과 같이 표현되는데, 이는 평면 $y=5$ 에 놓인 반지름이 $2$ 인 원을 의미한다.

$$\mathbf{\text{r}}(u,5)=<2\cos u,5,2\sin u>$$

그리고 이 것 역시 곡면이 아닌 곡선이다.

 

 

 

 

---

 

■ 매개변수 곡면의 접평면

 

곡면이 다음과 같이 매개변수 함수로 주어져 있다.

$$\mathbf{\text{r}}(u,v)=<x(u,v),y(u,v),z(u,v)>$$

 

 

$u=u_0$ 과 $v=v_0$ 이 교차하는 점인 $(u_0,v_0)$ 이 곡면에 대응 시키는 점을 $P_0$ 이라고 하자.

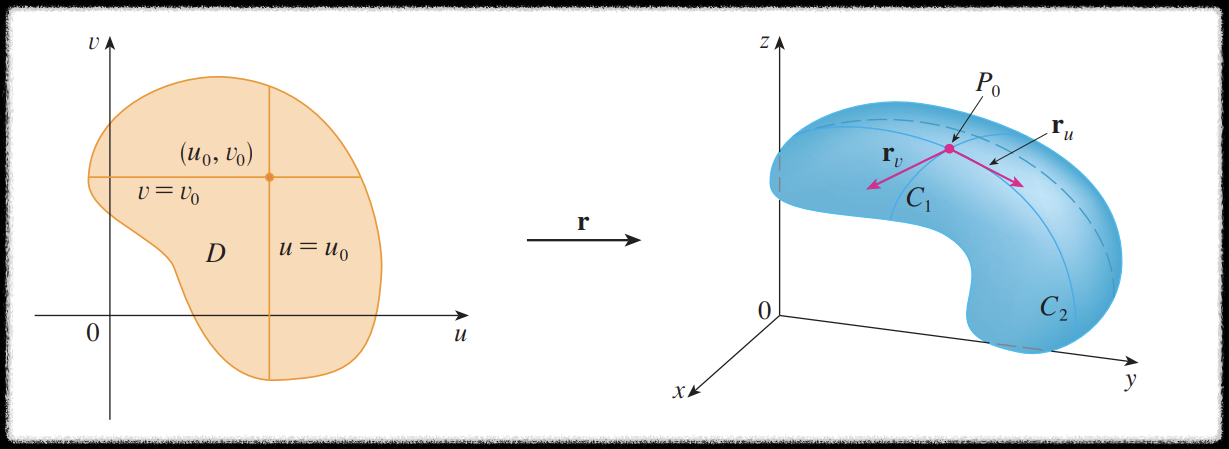
위 그림에서 정의역 $D$ 위의 직선 $u=u_0$ 이 대응시키는 곡면 위의 곡선은 오른쪽 그림처럼 $C_1$ 로 나타나 있고

직선 $v=v_0$ 이 대응시키는 곡면 위의 곡선은 $C_2$ 로 나타나 있다.

 

이 때 $\mathbf{\text{r}}(u,v)$ 의 $(u_0,v_0)$ 에서의

$u$ 에 대한 편도함수 ${\mathbf{\text{r}}}_u$ 는 점 $P_0$ 에서 곡선 $C_2$ 의 접선벡터를 나타내게 되고

$v$ 에 대한 편도함수 ${\mathbf{\text{r}}}_v$ 는 점 $P_0$ 에서 곡선 $C_1$ 의 접선벡터를 나타내게 된다.

 

이 두 접선벡터가 이루는 평면은 곡선의 $P_0$ 에서의 접평면이 되고

접평면의 방향(법선벡터)는 $\mathbf{\text{n}}=({\mathbf{\text{r}}}_u\times {\mathbf{\text{r}}}_v)(u_0,v_0)$ 가 된다.

그리고 점 $P_0$ 는 $(x(u_0,v_0),y(u_0,v_0),z(u_0,v_0))$ 이고 이는 접평면 위의 한 점이다.

 

접평면의 방향벡터 $\mathbf{\text{n}}$ 을 구했고, 지나는 한 점 $P_0$ 을 구했으므로 

평면의 벡터방정식으로 다음과 같이 접평면을 표현할 수 있다.

$$<P-P_0>\cdot \mathbf{\text{n}}=0$$

(여기서 $P$ 는 평면 위의 임의의 점 $(x,y,z)$ 이고 $<A-B>$ 는 두 점 $A,B$ 에 대해 $A-B$ 가 만드는 벡터이다.)

 

참고로 ${\mathbf{\text{r}}}_u\times {\mathbf{\text{r}}}_v\ne \mathbf{\text{0}}$ 이면 곡면은 부드럽다(smooth)고 정의한다.

 

 

예제 2

다음과 같이 주어진 매개곡면의 $(5,2,3)$ 위에서의 접평면의 방정식을 구하라
$$\{\begin{array}{l}x=u^2+1\\ y=v^3+1\\ z=u+v\end{array}$$

주어진 점 $(5,2,3)$ 을 만들기 위한 $u,v$ 값을 먼저 찾아보자.

$y=v^3+1=2$ 이므로 $v=1$ 을 우선 구할 수 있다.

$z=u+v=3$ 이므로 $u=2$ 임을 알 수 있다.

 

주어진 매개곡면을 $\mathbf{\text{r}}$ 라고 하면 $\mathbf{\text{r}}(u,v)$ 는 다음과 같으므로

$$\mathbf{\text{r}}(u,v)=<u^2+1,v^3+1,u+v>$$

$u$ 방향 도함수는 다음과 같고

$${\mathbf{\text{r}}}_u=<2u,0,1>$$

$v$ 방향 도함수는 다음과 같다.

$${\mathbf{\text{r}}}_v=<0,3v,1>$$

 

여기에 위에서 구한 $u=2,v=1$ 을 대입하면

$$\{\begin{array}{l}{\mathbf{\text{r}}}_u(2,1)=<4,0,1>\\ {\mathbf{\text{r}}}_v(2,1)=<0,3,1>\end{array}$$

이 둘을 외적하면 접평면의 법선 벡터가 나올 것이다.

$$\mathbf{\text{n}}={\mathbf{\text{r}}}_u(2,1)\times {\mathbf{\text{r}}}_v(2,1)=\left|\begin{array}{ccc}\mathbf{\text{i}}& \mathbf{\text{j}}& \mathbf{\text{k}}\\ 4& 0& 1\\ 0& 3& 1\end{array}\right|=<-3,-4,12>$$

 

평면의 법선벡터를 구했고 평면이 지나는 점을 알고 있으므로

평면의 벡터방정식을 다음과 같이 세울 수 있을 것이다.

$$<(x,y,z)-(5,2,3)>\cdot \mathbf{\text{n}}=0⟹<x-5,y-2,z-3>\cdot <-3,-4,12>=0$$

정리하면 다음과 같다.

$$3(x-5)+4(y-2)-12(z-3)=0$$

 

 

---

 

■ 매개변수 곡면의 넓이

 

이제는 매개변수 곡면의 넓이를 구하는 방법을 알아보자.

참고로 이 설명은 넓이를 계산하는 아이디어에 대한 스케치이지 증명을 한 것이 아니다.

 

 

단순한 상황을 가정하기 위해 $u,v$ 평면의 정의역이 다음 그림과 같이 사각형 영역이라고 해보자.

 

 

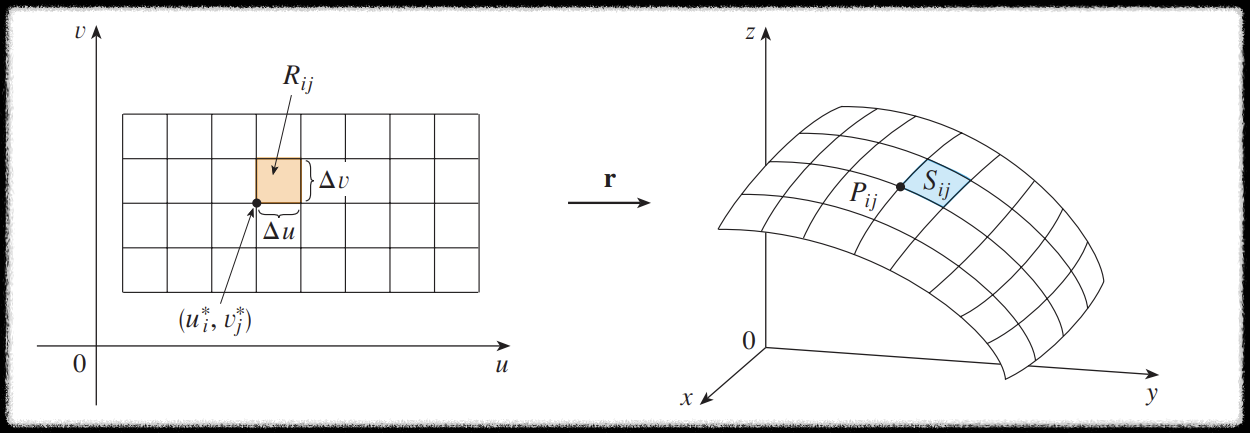
그리고 영역을 일정 간격 격자 형태로 나누어

$u$ 의 $i$ 번째, $v$ 의 $j$ 번째에 해당하는 조각 사각영역을 $R_{ij}$ 라고 하자.

$u_i^{\ast },v_j^{\ast }$ 를 $R_{ij}$ 의 왼쪽 아래 꼭지점으로 택하면 오른쪽 그림의 점 $P_{ij}$ 는 다음과 같다.

$$P_{ij}=\mathbf{\text{r}}(u_i^{\ast },v_j^{\ast })$$

그리고 이 점에서의 $\mathbf{\text{r}}$ 의 편도함수들을 다음과 같이 각각 표기 하자.

$$\{\begin{array}{l}{\mathbf{\text{r}}}_u^{\ast }={\mathbf{\text{r}}}_u(u_i^{\ast },v_j^{\ast })\\ {\mathbf{\text{r}}}_v^{\ast }={\mathbf{\text{r}}}_v(u_i^{\ast },v_j^{\ast })\end{array}$$

 

이제 조각 곡면 $S_{ij}$ 을 점 $P_{ij}$ 에서의 접평면 조각으로 근사시켜 넓이를 계산할 것이다.

 

 

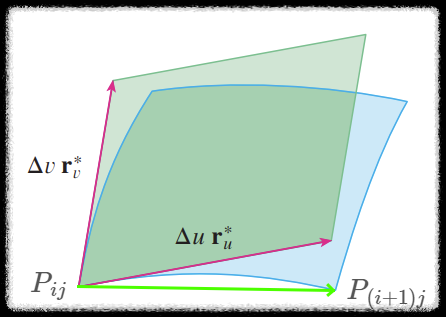
접평면 조각은 평행사변형 꼴을 하고 있으며 두 변의 길이는 각각 다음과 같이 둘 수 있다.

$$\mathrm{\Delta }u{\mathbf{\text{r}}}_u^{\ast },\mathrm{\Delta }v{\mathbf{\text{r}}}_v^{\ast }$$

변의 길이를 왜 저렇게 두어야 하는지는 벡터함수 곡선의 미분계수의 의미를 생각해보면 알 수 있다.

 

${\mathbf{\text{r}}}_u$ 는 $u$ 가 미세하게 변할 때, $\mathbf{\text{r}}$ 이 가리키는 위치의 변화(벡터)를 표현하는 식인데

말로 풀어쓰면 $u$ 당 벡터 $\mathbf{\text{r}}$ 의 변화 쯤으로 해석할 수 있다.

 

여기에 $\mathrm{\Delta }u$ 를 곱해준다면, $u$ 값이 $u_i^{\ast }$ 부터 $u_i^{\ast }+\mathrm{\Delta }u$ 까지 변할 때 $\mathbf{\text{r}}$ 의 변화의 근삿값을 의미하게 된다.

(위 사진에서 $\mathrm{\Delta }u{\mathbf{\text{r}}}_u^{\ast }$ 가 표시하는 붉은 화살표에 해당)

(변화의 근삿값 말고 실제 $\mathbf{\text{r}}$ 의 변화는 위 그림에서 $\overrightarrow{P_{ij}{P}_{(i+1)j}}$ 에 해당)

그리고 ${\mathbf{\text{r}}}_v$ 에 대해서도 똑같이 생각해주면 된다.

 

 

아무튼 위와 같은 이유로 곡선의 접평면 조각의 넓이는 다음과 같이 적을 수 있다.

$$\begin{array}{rl}{\text{Tangent Plane Area}}_{ij}=& |(\mathrm{\Delta }u{\mathbf{\text{r}}}_u^{\ast })\times (\mathrm{\Delta }v{\mathbf{\text{r}}}_v^{\ast })|\\ =& |{\mathbf{\text{r}}}_u^{\ast }\times {\mathbf{\text{r}}}_v^{\ast }|\mathrm{\Delta }u\mathrm{\Delta }v\end{array}$$

따라서 곡면 $S$ 의 넓이의 근삿값을 다음과 같이 접평면 조각의 넓이의 합으로 표현할 수 있다.

$$\text{Area}(S)\approx \sum _{i=1}^m\sum _{j=1}^n|{\mathbf{\text{r}}}_u^{\ast }\times {\mathbf{\text{r}}}_v^{\ast }|\mathrm{\Delta }u\mathrm{\Delta }v$$

이제 극한을 취해주면 다음과 같이 적분으로 나타낼 수 있다.

$$\text{Area}(S)={\iint }_D|{\mathbf{\text{r}}}_u\times {\mathbf{\text{r}}}_v|dudv$$

 

 

매개 곡면의 넓이의 정의

부드러운 매개 곡면 $S$ 가 다음과 같이 정의되어 있다고 하자.
$$\mathbf{\text{r}}(u,v)=<x(u,v),y(u,v),z(u,v)>,(u,v)\in D$$
영역 $D$ 의 점들이 곡면 $S$ 의 점들과 한 번씩만 대응된다고 할 때 $S$ 의 넓이는 다음과 같다.
$$\text{Area}(S)={\iint }_D|{\mathbf{\text{r}}}_u\times {\mathbf{\text{r}}}_v|dA$$

 

예제 3

두 곡선
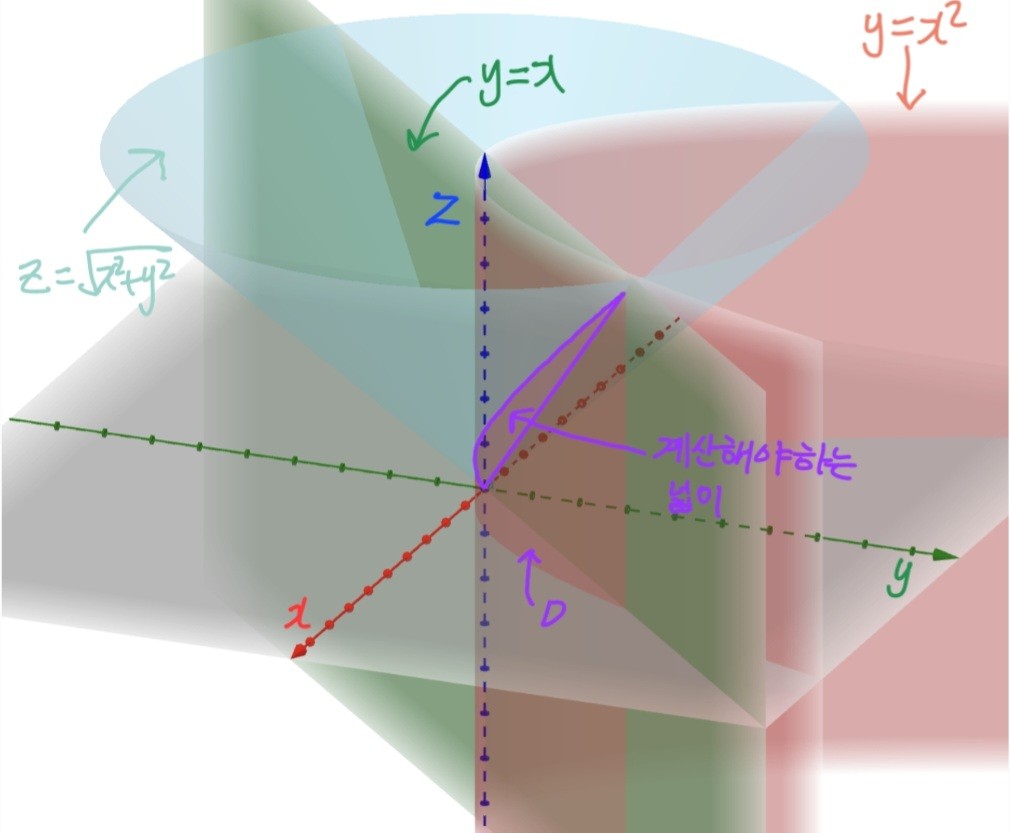
$y=x$,  $y=x^2$ 이 만드는 영역에서
곡면 $z=\sqrt{x^2+y^2}$ 의 넓이를 구하라

$u,v$ 얘기 하다가 갑자기 $x,y$ 얘기 한다고 당황할 필요가 없다.

그냥 $u,v$ 대신 $x,y$ 를 쓴 것과 같다고 생각하면 되고

 

곡면 $z=\sqrt{x^2+y^2}$ 는

$x$ 성분은 그냥 $x$

$y$ 성분도 그냥 $y$

$z$ 성분은 $\sqrt{x^2+y^2}$ 라고 생각하면 된다.

 

매개변수 벡터함수로 표현하자면 다음과 같이 쓸 수 있다.

$$\mathbf{\text{r}}(x,y)=<x,y,\sqrt{x^2+y^2}>$$

그러면 ${\mathbf{\text{r}}}_x$, ${\mathbf{\text{r}}}_y$ 는 각각 다음과 같고

$$\{\begin{array}{l}{\mathbf{\text{r}}}_x=<1,0,{\displaystyle \frac{x}{\sqrt{x^2+y^2}}}>\\ {\mathbf{\text{r}}}_y=<0,1,{\displaystyle \frac{y}{\sqrt{x^2+y^2}}}>\end{array}$$

이 둘을 외적하면 다음과 같다.

$${\mathbf{\text{r}}}_x\times {\mathbf{\text{r}}}_y=<-{\displaystyle \frac{x}{\sqrt{x^2+y^2}}},-{\displaystyle \frac{y}{\sqrt{x^2+y^2}}},1>$$

 

 

정의에 의해 곡면의 넓이는 $|{\mathbf{\text{r}}}_x\times {\mathbf{\text{r}}}_y|$ 를 적분한 것이므로 이를 계산해야 한다.

$$|{\mathbf{\text{r}}}_x\times {\mathbf{\text{r}}}_y|=\sqrt{1+{\left({\displaystyle \frac{x}{\sqrt{x^2+y^2}}}\right)}^2+{\left({\displaystyle \frac{y}{\sqrt{x^2+y^2}}}\right)}^2}=\sqrt{2}$$

 

 

이제 정의역을 살펴보자.

 

 

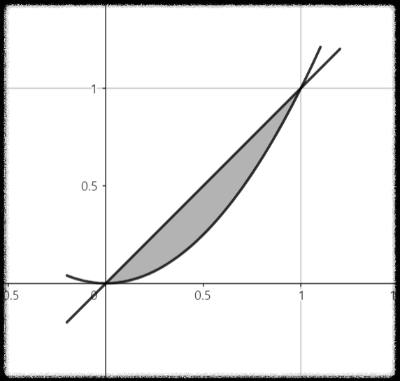
위 그림처럼 영역 $D$ 를 표시할 수 있는데, 식으로 표현하면 다음과 같다. 

$$D:0\le x\le 1,x^2\le y\le x$$

 

 

따라서 영역 $D$ 에서의 $\mathbf{\text{r}}$ 의 넓이는 다음과 같이 계산 된다.

$$\begin{array}{rl}\text{Area}={\iint }_D|{\mathbf{\text{r}}}_x\times {\mathbf{\text{r}}}_y|dA=& {\int }_0^1{\int }_{x^2}^x\sqrt{2}dydx\\ =& {\int }_0^1\sqrt{2}(x-x^2)dx\\ =& \sqrt{2}{[{\displaystyle \frac{x^2}{2}}-{\displaystyle \frac{x^3}{3}}]}_0^1={\displaystyle \frac{\sqrt{2}}{6}}\end{array}$$

 

 

 

아래는 이해를 돕기 위한 그림이다.