5. 함수의 기울기와 미분계수 (Slope and Derivative of a function)
6. 도함수와 미분가능성 (Derivative and Differentiability)
7. 미분 공식 (Differentiation Formulas)
9. 음함수의 미분법 (Implicit Differentiation)
10. 선형근사 (Linear Approximation)
와 관련된 문제들을 모아놓은 포스트이다.
가급적 위 포스트들을 모두 공부한 후 풀어보기를 권장한다.
좋은 문제들을 찾게된다면 추후에 계속 추가될 수 있다.

1. 다음 함수에서 $f'(0)$ 이 존재하는지 그렇지 않은지 결정하라. (스튜어트 연습문제)
$$ f(x) = \begin{cases} x\sin{\dfrac{1}{x}}, & x \neq 0 \\ 0, &x = 0 \end{cases} $$
풀이
미분계수의 정의에 의해 다음이 성립한다.
$$ f'(0) = \lim_{x \to 0} \dfrac{f(x) - f(0)}{x - 0} $$
여기서 극한 안에 들어있는 식은 극한의 정의에 의해 $x \neq 0$ 일 때의 값들이다. (기억이 안난다면 정의를 다시 살펴보고 오라.)
따라서 다음과 같다.
$$ \begin{align} f'(0) = &\lim_{x \to 0} \dfrac{x\sin{\dfrac{1}{x}}}{x} \\ = &\lim_{x \to 0} \sin{ \dfrac{1}{x} } \tag{$x \neq 0$ 이므로} \end{align} $$
그리고 이 극한은 수렴하지 않는다. 따라서 $x=0$ 에서 미분가능하지 않다.
아래는 극한이 존재하지 않는 이유의 증명이다.
극한이 다음과 같이 값 $L$ 에 수렴한다고 가정해보자.
$$ \lim_{x \to 0} \sin{\dfrac{1}{x}} = L $$
한편 $-1 \le \sin{\dfrac{1}{x}} \le 1$ 이므로 $|L| \le 1$ 이다.
이제 $|L| = 1$ 인 경우와 $|L| < 1$ 인 경우를 나눠서 생각해보자.
$|L| = 1$ 인 경우
극한의 정의에 의해 그 어떤 $\epsilon > 0$ 에 대해서도
$0 < |x| < \delta$ 인 범위에서 항상 $\left| \sin{\dfrac{1}{x}} - 1 \right| < \epsilon$ 을 만족하게 하는 $\delta >0$ 가 존재해야 한다.
하지만 $\sin$ 안의 변수가 $\dfrac{1}{x} = n\pi, \; (n \in \mathbb{N})$ 이면,
즉, $x = \dfrac{1}{n \pi}$ 이면 $\sin{\dfrac{1}{x}} = 0$ 을 만족하고
아무리 $\delta$를 작게 하여도 $0 < |x| < \delta$ 의 범위 안에 $x = \dfrac{1}{n\pi} \Longrightarrow \sin{\dfrac{1}{x}} = 0$ 을 만족하게 하는 $n$들이 존재한다.
따라서 $\epsilon = \dfrac{1}{2}$ (1보다 작은 어떤 양수여도 상관없다.) 라고 하면
$0 < |x| < \delta$ 인 범위에서 항상 $\left| \sin{\dfrac{1}{x}} - 1 \right| < \epsilon$ 을 만족하게 하는 $\delta >0$ 가 존재하지 않게 된다.
$|L| < 1$ 인 경우
극한의 정의에 의해 그 어떤 $\epsilon > 0$ 에 대해서도
$0 < |x| < \delta$ 인 범위에서 항상 $\left| \sin{\dfrac{1}{x}} - L \right| < \epsilon$ 을 만족하게 하는 $\delta >0$ 가 존재해야 한다.
한편 $\dfrac{1}{x} = 2n\pi + \dfrac{\pi}{2}, \; (n \in \mathbb{N}) $ 이면
즉 $x = \dfrac{2}{(4n+1)\pi}$ 이면 $\sin{\dfrac{1}{x}} = 1$ 을 만족한다.
역시 마찬가지로 아무리 작은 $\delta > 0$ 일지라도
$0 < |x| < \delta$ 일 때 $x = \dfrac{2}{(4n + 1)\pi} \Longrightarrow \sin{\dfrac{1}{x}} = 1$ 이게 하는 $n$들이 존재한다.
따라서 $L + \epsilon < 1$ 이게끔 하는 $\epsilon$ 에 대해서는 (오차범위 내에서 최대로 값을 올려도 1이 안되게 하는 오차 $\epsilon$ 을 설정하면)
$0 < |x| < \delta$ 인 범위에서 항상 $\left| \sin{\dfrac{1}{x}} - L \right| < \epsilon$ 을 만족하게 하는 $\delta >0$ 가 존재하지 않게 된다.
따라서 $|L| = 1$ 인 경우, $|L| < 1$ 인 경우를 종합하면 극한은 수렴하지 않는다는 결론을 내릴 수 있다.
2. $|x-6|$ 은 $x = 6$ 에서 미분가능하지 않음을 보여라. (스튜어트 연습문제)
풀이
$f(x) = |x-6|$ 이라 하자. 그러면 다음과 같이 표현될 수 있다.
$$ f(x) = \begin{cases} x-6 &(x \geq 6) \\ -x+6 &(x < 6) \end{cases} $$
$f$ 가 $x=6$ 에서 미분가능하려면 미분계수의 정의에 의해 다음의 극한이 존재해야 한다.
$$ \begin{align} f'(6) = &\lim_{x \to 6} \dfrac{f(x) - f(6)}{x-6} \\ = &\lim_{x \to 6} \dfrac{|x-6| - 0}{x - 6} = \lim_{x \to 6} \dfrac{|x-6|}{x-6} \end{align} $$
이제 이 극한이 존재하는지 보려면 $6$ 에서의 좌극한 우극한이 같은 값으로 수렴하는지 살펴봐야 한다.
$(x \geq 6)$ 인 경우
$$\lim_{x \to 6+} \dfrac{x-6}{x-6} = \lim_{x \to 6+} 1 = 1$$
$(x < 6)$ 인 경우
$$\lim_{x \to 6-} \dfrac{-x+6}{x-6} = \lim_{x \to 6-} -1 = -1$$
좌극한 우극한이 같지 않으므로 $\lim\limits_{x \to 6} \dfrac{|x-6|}{x-6}$ 은 존재하지 않는다.
따라서 미분가능하지 않다.
3. 다음을 계산하라. (스튜어트 연습문제)
$$ \lim_{x \to 1} \dfrac{x^{1000} - 1}{x-1} $$
풀이
식의 형태가 미분계수의 계산 꼴이랑 유사하다는 점을 주목하자.
주어진 식은 $f(x) = x^{1000}$ 의 $1$ 에서의 미분계수를 구하는 식과 같다.
한편 $f(x)$ 는 다항식이므로 실수 전체에서 미분 가능하고 따라서 $f'(1)$ 이 존재한다.
다항식의 미분공식을 적용하면
$$f'(x) = 1000x^{999}$$
$$ \therefore f'(1) = 1000 $$
4. 다음 함수가 어디에서 미분가능한지 구하라. (스튜어트 연습문제)
$$ h(x) = |x-1| + |x+2| $$
풀이
$|x - 1|$ 은 $x = 1$ 을 기준으로 양수 음수가 나뉜다.
$|x + 2|$ 는 $x - 2$ 를 기준으로 양수 음수가 나뉜다.
따라서 함수를 다음과 같이 세 구간으로 나누어 생각해볼 수 있다.
$$ h(x) = \begin{cases} -(x-1) - (x+2) & (x < -2) \\ -(x-1) + (x+2) & (-2 \le x < 1) \\ (x-1) + (x + 2) & (1 \le x) \end{cases} $$
$$ \therefore h(x) = \begin{cases} -2x-1 & (x < -2) \\ 3 & (-2 \le x < 1) \\ 2x + 1 & (1 \le x) \end{cases} $$
각 구간의 함수들은 다항함수이거나 상수함수이므로 구간의 경계점을 제외하는 구간들인
$(-\infty, -2), (-2, 1), (1, \infty)$ 에서는 미분 가능하다.
따라서 $-2, 1$ 에서의 미분가능성만 확인하면 된다.
$x = -2$ 인 경우
좌미분계수의 정의에 의해 좌미분계수는 다음과 같다. 이 경우는 $(x < -2)$ 일 때를 생각한다.
$$ \lim_{x \to (-2)-} \dfrac{(-2x - 1) - (3)}{x + 2} = \lim_{x \to (-2)-} \dfrac{-2x-4}{x+2} = \lim_{x \to (-2)-} -2 = -2 $$
우미분계수의 정의에 의해 우미분계수는 다음과 같다. 이 경우는 $(x > 2)$ 일 때를 생각한다.
$$ \lim_{x \to (-2)+} \dfrac{(3) - (3)}{x + 2} = \lim_{x \to (-2)+} 0 = 0 $$
좌우 미분계수가 다른 값으로 수렴하므로 $x=-2$ 에서 미분계수는 존재하지 않는다.
$x = 1$ 인 경우
좌미분계수의 정의에 의해 좌미분계수는 다음과 같다. 이 경우는 $(x < 1)$ 일 때를 생각한다.
$$ \lim_{x \to 1-} \dfrac{(3) - (3)}{x - 1} = \lim_{x \to 1-} 0 = 0 $$
우미분계수의 정의에 의해 우미분계수는 다음과 같다. 이 경우는 $(x > 1)$ 일 때를 생각한다.
$$ \lim_{x \to 1+} \dfrac{(2x+1) - (3)}{x - 1} = \lim_{x \to 1+} \dfrac{2x-2}{x-1} = \lim_{x \to 1+} 2 = 2 $$
좌우 미분계수가 다른 값으로 수렴하므로 $x=1$ 에서 미분계수는 존재하지 않는다.
따라서 $h(x)$ 가 미분가능한 구간은 $(-\infty, -2), (-2, 1), (1, \infty)$ 이다.
5. 다음 극한을 계산하라. (스튜어트 연습문제)
$$ \lim_{x \to 1} \dfrac{ \sin{(x-1)} }{x^2 + x - 2} $$
풀이
$$ \lim_{x \to 1} \dfrac{ \sin{(x-1)} }{x^{2} + x - 2} = \lim_{x \to 1} \left[ \dfrac{ \sin{(x-1)} }{x - 1} \cdot (x + 2) \right] $$
이 때 $\lim\limits_{x \to 1} \dfrac{ \sin{(x-1)} }{x-1}$ 이 수렴하고 $\lim\limits_{x \to 1} (x+2)$ 가 수렴한다면
극한법칙에 의해 이들의 곱으로 분리할 수 있을것이다.
첫 번째 극한을 보면 미분계수의 꼴이랑 유사하다는 점을 알 수 있다.
그리고 $f(x) = \sin{(x - 1)}$ 로 표현되는 함수의 $x = 1$ 에서의 미분계수를 구해보면 다음과 같다.
$$ f'(1) = \lim_{x \to 1} \dfrac{f(x) - f(1)}{x-1} = \lim_{x \to 1} \dfrac{ \sin{(x-1)} - 0 }{x - 1} = \lim_{x \to 1} \dfrac{ \sin{(x-1)} }{x-1} $$
이는 첫 번째 극한이랑 일치한다.
따라서 첫 번째 극한은 $f(x) = \sin{(x-1)}$ 의 $x=1$ 에서의 미분 계수와 같고
사인 함수는 실수 전체에서 미분 가능하므로 극한은 수렴한다.
이제 수렴값을 구해보자. 사인함수의 미분공식과 연쇄법칙을 적용하면 $f'(x) = \cos{(x-1)}$ 이므로
$ f'(1) = \cos{0} = 1 $
($x - 1$ 을 $t$ 로 치환하여 $\lim\limits_{t \to 0} \dfrac{\sin{t}}{t} = 1$ 을 이용해도 된다.)
두 번째 극한 역시 $\lim\limits_{x \to 1} (x+2) = 3$ 으로 수렴한다.
따라서 다음이 성립한다.
$$ \begin{align} \lim_{x \to 1} \dfrac{ \sin{(x-1)} }{x^{2} + x - 2} = &\lim_{x \to 1} \left[ \dfrac{ \sin{(x-1)} }{x - 1} \cdot (x + 2) \right] \\ = &\left[ \lim_{x \to 1} \dfrac{ \sin{(x-1)} }{x-1} \right] \cdot \left[ \lim_{x \to 1} (x+2) \right] \\ = &1 \times 3 \\ = &\textcolor{red}{3} \end{align} $$
6. 곡선 $x^{3} + y^{3} = 6xy$ 위의 점 $(3, 3)$ 에서의 접선의 방정식을 구하시오. (고려대학교 편입 비수학과 2018 기출)
풀이
음함수 미분으로 $x = 3$ 에서의 미분계수를 구해보자.
$y$ 를 $x$ 의 함수로 보면 다음과 같이 표현할 수 있다.
$$ x^{3} + [y(x)]^{3} = 6x[y(x)] $$
다음과 같이 양변을 $x$ 에 대해 미분하고 $y'$ 에 대해 정리해보자.
$$ \begin{align} &\dfrac{d}{dx} [x^{3} + [y(x)]^{3}] = \dfrac{d}{dx}[6x[y(x)]] \\ \Longleftrightarrow &3x^{2} + 3[y(x)]^{2}y'(x) = 6y(x) + 6x[y'(x)] \\ \Longleftrightarrow &[3[y(x)]^{2} - 6x]y'(x) = 6y(x) - 3x^{2} \\ \Longleftrightarrow &y'(x) = \dfrac{6y(x) - 3x^{2}}{3[y(x)]^{2} - 6x} \end{align} $$
한편 $x = 3$ 이면 $y = 3$ 이므로 $y(3) = 3$ 이다.
$$ \therefore y'(3) = \dfrac{6 \times 3 - 3 \times 3^{2} }{3\times 3^{2} - 6 \times 3} = -1 $$
$(3, 3)$ 을 지나고 기울기가 $-1$ 인 접선의 방정식은 다음과 같다.
$$ y - 3 = -(x-3) $$
정리하면
$$ y = -x + 6 $$
7. 다음 극한을 계산하라. (스튜어트 연습문제)
$$ \lim_{x \to 0} \csc{x} \sin{(\sin{x})} $$
풀이
주어진 식은 다음과 같다.
$$ \lim_{x \to 0} \dfrac{\cos{x}}{\sin{x}} \sin{(\sin{x})} = \lim_{x \to 0} \left[ \cos{x} \cdot \dfrac{ \sin{(\sin{x})} }{\sin{x}} \right] $$
$ \lim\limits_{x \to 0} \cos{x} $ 이 수렴하고 $ \lim\limits_{x \to 0} \dfrac{ \sin{(\sin{x})} }{\sin{x}} $ 이 수렴한다면 극한법칙에 의해 이 둘의 곱으로 분리될 것이다.
한편 $\sin{x} = t$ 로 치환하면 $t$ 는 $x$ 에 대한 사인함수이고 실수 전체에서 연속이다.
따라서 $ \lim\limits_{x \to 0} \sin{x} = \sin{0} = 0 $ 이고 이는 $x \to 0$ 이면 $t \to 0$ 임을 의미한다.
따라서 다음이 성립한다.
$$ \lim_{x \to 0} \dfrac{ \sin{(\sin{x})} }{\sin{x}} = \lim_{t \to 0} \dfrac{\sin{t}}{t} = 1 $$
또 한편 다음 식이 성립한다.
$$ \lim_{x \to 0} \cos{x} = 1 $$
분리된 극한이 모두 수렴하므로 극한법칙에 의해 다음이 성립한다.
$$ \begin{align} \lim_{x \to 0} \left[ \cos{x} \cdot \dfrac{ \sin{(\sin{x})} }{\sin{x}} \right] = &\left[ \lim_{x \to 0} \cos{x} \right] \cdot \left[ \lim_{x \to 0} \dfrac{ \sin{(\sin{x})} }{\sin{x}} \right] \\ = &1 \times 1 \\ = &\textcolor{red}{1} \end{align} $$
8. $(1, 1)$ 근방에서 $x^{3} + x^{2}y + xy^{3} = 3$ 을 만족하는 함수 $y = f(x)$ 에 대해 $f''(1)$ 의 값을 구하시오. (고려대학교 편입 2019 기출)
풀이
음함수 미분법을 이용해 $f''(1)$ 을 구해보자.
$f''(x) = \dfrac{d}{dx}f'(x)$ 이므로 $f'(x)$ 를 먼저 구한다.
$y$ 를 $x$ 에 대한 함수로 보고 양변을 $x$ 로 미분하자.
$$ \begin{align} &\dfrac{d}{dx}[ x^{3} + x^{2}y + xy^{3} ] &=& \dfrac{d}{dx} [3] \\ \Longrightarrow &3x^2 + 2xy + x^{2}y' + y^3 + 3xy^{2}y' &=& 0 \\ \Longleftrightarrow &(x^{2} + 3xy^{2})y' + (3x^{2} + 2xy + y^{3}) &=& 0 \tag{식 1} \end{align} $$
이를 $y'$ 에 대해 정리하면 다음과 같다.
$$ \begin{align} y' = -\dfrac{ 3x^{2} + 2xy + y^{3} }{ x^{2} + 3xy^{2} } \tag{식 2} \end{align} $$
$x= 1$ 일 때 $y = 1$ 이므로 이를 대입하면
$$ y'(1) = f'(1) = -\dfrac{3}{2} $$
이제 $y'$ 를 $x$ 에 대해 한 번 더 미분하여 $y''$ 를 얻을 수 있다.
그러기 위해서는 $(식 2)$ 를 $x$ 에 대해 몫의 미분을 해야 하지만, 이는 식이 복잡하다.
$(식 1)$ 의 양변을 미분해도 $y''$ 를 얻어낼 수 있는데, 이 쪽이 더 간단하다. $(식 1)$ 의 양변을 미분하자.
$$ \begin{align} (2x + 3y^{2} + 6xyy')y' + (x^{2} + 3xy^{2})y'' + (6x + 2y + 2xy' + 3y^{2}y') \end{align} $$
이 식을 다 전개해서 정리할 필요 없다.
구하는것은 $f''(1)$ 이므로 $f'(1) = y'(1) = -\dfrac{3}{2}$ 을 아는 이 시점에서는
$x = 1$, $y = 1$, $y' = -1$ 을 대입하기만 하면 된다.
이를 대입하여 정리하면 최종적으로 다음을 얻는다.
$$ y''(1) = f''(1) = -\dfrac{13}{8} $$
9. 다음 그림은 중심각 $\theta$ 에 대응하는 길이 $s$ 인 원호와 길이 $d$ 인 현을 나타낸다.
$\lim\limits_{\theta \to 0+} \dfrac{s}{d}$ 를 구하라.

풀이
원의 반지름이 $r$ 이라 가정하자.
반지름이 $r$ 이고 중심각이 $\theta$ 인 호의 길이는 $r\theta$ 이다.
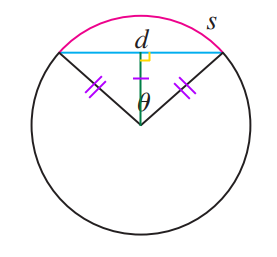
그리고 위 그림과 같이 원의 중심에서 현에 수선을 내리면
수선에 의해 나눠진 두 삼각형에서 빗변의 길이는 반지름 $r$ 로 같고
수선의 길이는 공통이며 직각삼각형이므로
나뉜 두 삼각형은 RHS 합동이다.
따라서 수선에 의해 각 $\theta$ 는 이등분되며
현의 길이는 $2 \times r\sin{\dfrac{\theta}{2}}$ 로 표현된다.
따라서 다음과 같다.
$$ \lim_{\theta \to 0+} \dfrac{s}{d} = \lim_{\theta \to 0+} \dfrac{r\theta}{2r\sin{\dfrac{\theta}{2}}} = \lim_{\theta \to 0+} \dfrac{\dfrac{\theta}{2}}{\sin{\dfrac{\theta}{2}}} $$
$\dfrac{\theta}{2} = t$ 로 치환하면 $t$ 는 $\theta$ 에 대한 다항함수이므로 연속이다.
따라서 $\theta \to 0+$ 이면 $t \to 0+$ 이고 다음과 같은 식으로 쓸 수 있다.
$$ \lim_{\theta \to 0+} \dfrac{\dfrac{\theta}{2}}{\sin{\dfrac{\theta}{2}}} = \lim_{t \to 0+} \dfrac{t}{\sin{t}}$$
한편 $\lim\limits_{t \to 0} \dfrac{\sin{t}}{t} = 1$ 임을 안다.
따라서 $\lim\limits_{t \to 0+} \dfrac{\sin{t}}{t} = 1$ 이고 극한법칙에 의해 다음이 성립한다.
$$ \lim_{t \to 0+} \dfrac{t}{\sin{t}} = \lim_{t \to 0+} \dfrac{1}{\dfrac{\sin{t}}{t}} = \dfrac{\lim\limits_{t \to 0+} 1 }{ \lim\limits_{t \to 0+} \dfrac{\sin{t}}{t} } = \dfrac{1}{1} = 1 $$
$$ \therefore \lim_{\theta \to 0+} \dfrac{s}{d} = 1 $$
10. 다음 극한을 계산하라. (스튜어트 연습문제)
$$ \lim_{x \to 0} \dfrac{\sqrt{1+\tan{x}} - \sqrt{1+\sin{x}} }{x^{3}} $$
풀이
루트는 직접 처리하기가 곤란하다.
이런식으로 비슷한 꼴의 차로 이루어진 분수식을 본다면 곱셈공식의 합차공식을 이용하여
유리화를 시도해보아야 한다.
주어진 식은 다음과 같다.
$$ \begin{align} \lim_{x \to 0} \dfrac{\sqrt{1 + \tan{x}} - \sqrt{1 + \sin{x}} }{ x^{3} } = &\lim_{x \to 0} \dfrac{ (\sqrt{1 + \tan{x}} - \sqrt{1 + \sin{x}}) \cdot (\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}}) }{ x^{3} (\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}} ) } \\ = &\lim_{x \to 0} \dfrac{ (1 + \tan{x}) - (1 + \sin{x}) }{ x^{3} (\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}} ) } \\ = &\lim_{x \to 0} \dfrac{ \tan{x} - \sin{x} }{ x^{3} (\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}} ) } \\ = &\lim_{x \to 0} \textcolor{pink}{ \dfrac{\sin{x}}{x}} \cdot \textcolor{skyblue}{\dfrac{\sec{x} - 1}{x^{2}}} \cdot \textcolor{orange}{\dfrac{1}{\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}} }} \end{align} $$
$ \textcolor{pink}{\lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1} $ 이고
$ \textcolor{orange}{ \lim\limits_{x \to 0} \dfrac{1}{\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}}} = \dfrac{1}{2} } $ 으로 수렴한다.
따라서 가운데의 식
$ \textcolor{skyblue}{\lim\limits_{x \to 0} \dfrac{\sec{x} - 1}{ x^{2} } } $ 이 수렴한다면 극한법칙에 의해 세 극한의 곱으로 분리할 수 있을 것이다.
한편 $\sec{x} - 1$ 을 보면 항등식 $\sec^{2}{x} - 1 = \tan^{2}{x}$ 가 왠지 떠오른다.
이것을 만들기 위해 $\dfrac{\sec{x} - 1}{x^{2}}$ 의 분모분자에 $\sec{x} + 1$ 을 곱해 합차공식을 또 이용하자.
$$ \begin{align} \textcolor{skyblue}{\lim_{x \to 0} \dfrac{\sec{x} - 1}{x^{2}}} = &\lim_{x \to 0} \dfrac{ (\sec{x} - 1) \cdot (\sec{x} + 1) }{ x^{2} (\sec{x} + 1) } \\ = &\lim_{x \to 0} \dfrac{ \sec^{2}{x} - 1 }{x^{2}(\sec{x} + 1)} \\ = &\lim_{x \to 0} \dfrac{\tan^{2}{x}}{x^{2}} \cdot \dfrac{1}{\sec{x} + 1} \end{align} $$
한편 $\lim\limits_{x \to 0} \dfrac{\tan{x}}{x} = \lim\limits_{x \to 0} \dfrac{\sin{x}}{x} \cdot \sec{x} $ 이고
$\lim\limits_{x \to 0} \dfrac{\sin{x}}{x} = 1$ 이고 $\lim\limits_{x \to 0} \sec{x} = 1$ 이므로
$\lim\limits_{x \to 0} \dfrac{\tan{x}}{x} = 1$ 이다.
또 $\lim\limits_{x \to 0} \dfrac{1}{\sec{x} + 1} = \dfrac{1}{2} $ 이므로 극한법칙에 의해 다음이 성립한다.
$$ \textcolor{skyblue}{\lim_{x \to 0} \dfrac{\sec{x} - 1}{x^{2}}} = \lim_{x \to 0} \dfrac{\tan^{2}{x}}{x^{2}} \cdot \dfrac{1}{\sec{x} + 1} = 1^{2} \times \dfrac{1}{2} = \textcolor{skyblue}{\dfrac{1}{2}} $$
따라서 극한법칙에 의해 다음이 성립한다.
$$ \begin{align} \lim_{x \to 0} \dfrac{\sqrt{1 + \tan{x}} - \sqrt{1 + \sin{x}} }{ x^{3} } = &\lim_{x \to 0} \textcolor{pink}{ \dfrac{\sin{x}}{x}} \cdot \textcolor{skyblue}{\dfrac{\sec{x} - 1}{x^{2}}} \cdot \textcolor{orange}{\dfrac{1}{\sqrt{1 + \tan{x}} + \sqrt{1 + \sin{x}} }} \\ = &1 \times \dfrac{1}{2} \times \dfrac{1}{2} \\ = &\textcolor{red}{\dfrac{1}{4}} \end{align} $$
11. 선형근사를 이용하여 $e^{0.01}$ 의 근삿값을 구하시오. (연세대학교 편입 2007 기출)
풀이
적절한 함수를 설정해야 한다. $f(x) = e^{x}$ 면 적당할 것 같다.
$f'(x) = e^{x}$ 이므로 $f'(0) = 1$, $f(0) = 1$ 이므로 $x = 0$ 에서의 $f$ 의 선형화는 다음과 같다.
$$ L(x) = f(0) + f'(0)(x - 0) = 1 + x $$
따라서 $e^{0.01}$ 의 선형근사는 다음과 같다.
$$ e^{0.01} \approx L(0.01) = 1 + 0.01 = 1.01 $$
Wolfram Alpha 로 실제값을 구해보면 $e^{0.01} = 1.0100502...$ 로 선형근사와의 오차가 매우 작다.
12. $\sqrt{99}$ 를 선형근사를 이용하여 근사적으로 구하시오. (연세대학교 편입 수학과 2012 기출)
풀이
적절한 함수를 설정해야 한다. $f(x) = \sqrt{x}$ 면 적당하다.
$f'(x) = \dfrac{1}{2\sqrt{x}}$ 이므로 $f'(100) = \dfrac{1}{20}$ 이고 $f(100) = 10$ 이므로
$x = 100$ 에서의 $f$ 의 선형화는 다음과 같다.
$$ L(x) = f(100) + f'(100)(x-100) = 10 + \dfrac{1}{20}(x-100) $$
따라서 $\sqrt{99}$ 의 선형근사는 다음과 같다.
$$ \sqrt{99} \approx L(99) = 10 + \dfrac{1}{20}(99 - 100) = 9.95$$
Wolfram Alpha 로 실제값을 구해보면 $\sqrt{99} = 9.94987$ 로 선형근사값과 매우 유사하다.
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 12. 롤의 정리, 평균값 정리 (Rolle's Theorem, Mean Value Theorem) (0) | 2021.02.18 |
|---|---|
| 11. 최댓값, 최솟값, 극값정리, 페르마 정리 (Maximum, Minimum, Extreme Value Theorem, Fermat's Theorem) (0) | 2021.01.27 |
| 10. 선형근사 (Linear Approximation) (2) | 2021.01.22 |
| 9. 음함수의 미분법 (Implicit Differentiation) (0) | 2021.01.21 |
| 8. 연쇄 법칙과 증명 (Chain Rule) (10) | 2021.01.19 |