
이제는 앞서서 배운 미분을 이용해 함수의 개형을 파악하는 방법을 알아볼것이다.
자연과학 뿐만 아니라 사회과학, 경제학 등 다양한 분야에서 그래프의 개형을 파악하는것은 중요한 일이다.
그리고 이 과정에서 그래프의 최고점, 최저점이 어디인지 알아볼 필요도 있을 것이다.
이를 위해서 최댓값과 최솟값의 정의를 정확히 해 둘 필요가 있다.
최댓값, 최솟값의 정의
$c$ 가 $f$ 의 정의역 $D$ 에 속한 수라고 하자.
그러면 $f(c)$ 는 다음과 같다.
■ $D$ 에 속하는 모든 $x$ 에 대해 $f(c) \geq f(x)$ 이면 $D$ 에서 $f$ 의 최댓값이다.
■ $D$ 에 속하는 모든 $x$ 에 대해 $f(c) \le f(x)$ 이면 $D$ 에서 $f$ 의 최솟값이다.
그리고 정의역 전체에서 최댓값 최솟값인 경우 말고
정의역 내의 일부 구간에서 최댓값, 일부 구간에서의 최솟값에 대해 생각해 볼 수도 있을것이다.
이를 각각 극댓값, 극솟값이라 부른다.
참고로 이들을 영어로는 Local Maximum, Local Minimum 이라 부르는데,
전체 구역(Global) 이 아닌 일부 구역(Local) 에서 최대 또는 최솟값을 갖는다는 의미에 잘 부합한다.
극댓값, 극솟값의 정의
수 $f(c)$ 는 다음과 같다.
■ $x$ 가 $c$ 를 포함하는 어떤 개구간에서 $f(c) \geq f(x)$ 이면 $f$ 의 극댓값이다.
■ $x$ 가 $c$ 를 포함하는 어떤 개구간에서 $f(c) \le f(x)$ 이면 $f$ 의 극솟값이다.
쉽게 얘기해서 어떤 점 주변에 아무런 크기의 범위를 잡아서
그 점이 그 범위 내에서 최댓값이게 되면 그 값을 극댓값이라 부른다.
다음 그래프들을 보며 최대, 최솟값, 극대, 극솟값이 어떤 점인지 살펴보자.

$x = 0$ 에서 최솟값이자 극솟값인 $0$ 을 갖는다.

최댓값, 최솟값은 존재하지 않는다.
그리고 어떤 개구간을 잡아도 그 구간 내에서 국소적인 최댓값, 최솟값을 정할 수 없다.
따라서 극댓값, 극솟값 역시 존재하지 않는다.
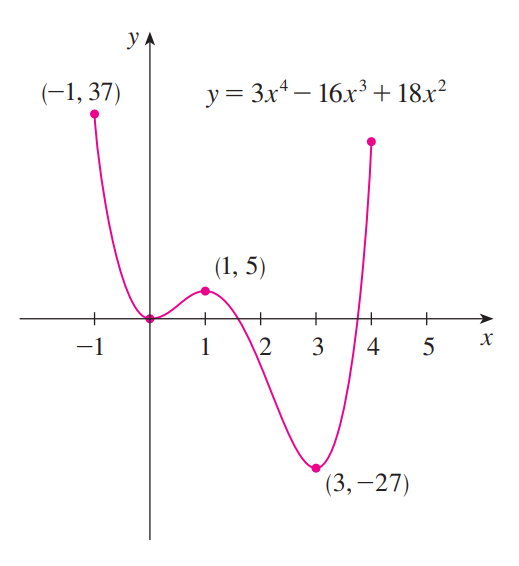
최솟값은 $x = 3$ 일 때 $-27$ 이다.
이는 극솟값이기도 하다.
$f(-1) = 37$, $ f(4) = 32 $ 이므로
$[1, 4]$ 에서 정의된 이 함수는
$x = -1$ 에서 최댓값 $37$ 을 갖는다.
참고로 이것은 극댓값은 아니다.
그리고 $x = 1$ 에서 극댓값 $5$ 를 갖고
$x = 0$ 에서 극솟값 0을 갖는다.
아래에 소개할 두 정리는 최대, 최소, 극대, 극소에 관련된 정리들이다.
첫번째로 소개할 다음 정리는 어떤 함수가 극값을 갖는다는 것을 보장하는 조건이다.
극값 정리
함수 $f$ 가 폐구간 $[a,b]$ 에서 연속이면,
$f$ 는 $[a, b]$ 의 어떤 수 $c$ 와 $d$ 에서 최댓값 $f(c)$ 와 최솟값 $f(d)$ 를 갖는다.
쉽게 얘기하면,
폐구간에서 연속이면 그 구간 내에서는 항상 최댓값과 최솟값이 존재한다는 말이다.
이 정리가 나중에 나올 많은 정리들을 증명할 때 자주 등장하므로 잘 숙지해두면 좋다.
어떻게 보면 당연해보이는 이 정리의 증명은 스튜어트 미적분학의 범위를 뛰어넘으므로 생략한다.
페르마 정리
$f$ 가 $c$ 에서 극대 또는 극소이고 $f'(c)$ 가 존재하면 $f'(c) = 0$ 이다.
증명
$f$ 가 $c$ 에서 극대라고 가정하자.
그러면 극대의 정의에 의해 $c$ 에 충분히 가까운 $x$ 에 대해 $f(c) \geq f(x)$ 이다.
이는 $h \neq 0$ 에 대해 다음이 성립함을 의미한다.
$$ f(c) \geq f(c + h) $$
$$ \Longleftrightarrow f(c+h) - f(c) \le 0 \tag{식 1} $$
이제 $h > 0$ 이라 가정하여 $h$ 로 나누면 다음이 성립한다.
$$ \dfrac{f(c+h) - f(c)}{h} \le 0 $$
이 부등식의 양변에 우극한을 취하면 다음을 얻는다. 이는 $f$ 의 우미분계수 식과 같다.
$$ \lim_{h \to 0+} \dfrac{f(c+h) - f(c)}{h} \le 0 $$
한편 $f'(c)$ 가 존재하므로 우미분계수는 미분계수랑 같다. 따라서 다음이 성립한다.
$$ f'(c) = \lim_{h \to 0} \dfrac{f(c + h) - f(c)}{h} = \lim_{h \to 0+} \dfrac{f(c+h) - f(c)}{h} $$
따라서 $f'(c) \le 0$ 이다.
이제 $h < 0$ 이라 가정하면 $(식 1)$ 에서 $h$ 를 나눌 때 부등호 방향이 반대이다.
$$ \dfrac{f(c + h) - f(c)}{h} \geq 0 $$
이 부등식의 양변에 좌극한을 취하면 다음을 얻는다. 이는 $f$ 의 좌미분계수 식과 같다.
$$ \lim_{h \to 0+} \dfrac{f(c+h) - f(c)}{h} \geq 0 $$
$f'(c)$ 가 존재하므로 역시 다음이 성립한다.
$$ f'(c) = \lim_{h \to 0} \dfrac{f(c + h) - f(c)}{h} = \lim_{h \to 0-} \dfrac{f(c+h) - f(c)}{h} $$
따라서 $f'(c) \geq 0$ 이다.
$f'(c) \le 0$ 이고 $f'(c) \geq 0$ 이므로 이를 동시에 만족하려면 $f'(c) = 0$ 이다.
$f$ 가 $c$ 에서 극소인 경우도 유사한 방법으로 증명할 수 있다.

참고로 이 정리의 역은 거짓이다.
쉬운 예로 $y = x^{3}$ 의 경우에 $f'(0) = 0$ 이지만
$f(0)$ 은 극대도 아니고 극소도 아니다.

이제 앞서 언급한 극값 정리, 페르마 정리를 이용하여
폐구간 $[a, b]$ 에서 연속인 함수의 최댓값, 최솟값을 구하는 방법을 알아볼 것이다.
우선 함수가 주어진 폐구간에서 연속이라면
극값 정리에 의해 구간 내에서 항상 최솟값과 최댓값을 갖는다는것을 보장한다.
그리고 최솟값, 최댓값이 될 수 있는 후보는 특정 구간에서의 최대 최소인 극대, 극소점이 유력한 후보일 것이다.
한편, 구간의 끝점은 극대 또는 극솟값이 될 수 없지만 최댓값 또는 최솟값이 나올 수는 있는 점들이다.
따라서 최솟값 최댓값 후보에 구간의 끝 점도 넣어야 할 것이다.
정리하자면 폐구간에서 연속인 함수에서 최대 최솟값의 후보들은 다음과 같다.
1. 극대점, 극소점
2. 구간의 양 끝 점
한편 연속인 구간은 미분가능한 구간과 미분가능하지 않지만 연속인 구간들로 이루어져 있을 것이다.
미분가능한 부분 구간에서는 페르마 정리에 의해 어디가 극대 또는 극소점인지 쉽게 구할 수 있다.
페르마 정리에 의해 극대 또는 극소인 점 $c$ 에서 무조건 $f'(c) = 0$ 가 성립하고
따라서 $f'(c) = 0$ 인 점들만 살펴보면 모든 극대 또는 극소일 수 있는 점을 살펴보게 되는 것이다.
하지만 나머지 미분가능하지 않은 연속인 부분구간에서는 이러한 손쉬운 방법이 존재하지 않으므로
이러한 미분불가능 점들은 극대극소 후보로 모두 고려해야한다.
이 둘을 한 번에 묶어 좀 더 쉽게 정리를 만들기 위해 임계수(critical number) 라는 개념을 도입하자.
임계수(Critical number)의 정의
함수 $f$ 의 임계수는 $f'(c) = 0$ 이거나 $f'(c)$가 존재하지 않게 하는 정의역 속의 수 $c$ 를 말한다.
이 개념을 이용하면 폐구간에서 연속인 함수에서 최댓값 최솟값을 찾는 법은 다음과 같이 정리 할 수 있다.
폐구간 방법
폐구간 $[a, b]$ 에서 연속인 함수 $f$ 의 최댓값 또는 최솟값을 구하기 위해서는
1. $(a, b)$ 에 있는 $f$ 의 임계수에서의 함숫값을 구한다.
2. 구간의 양 끝점에서 함숫값을 구한다.
1, 2 번에서 구한 함숫값들 중 제일 큰 값이 최댓값이고 제일 작은 값이 최솟값이다.
예제
다음과 같은 조각으로 정의된 함수가 있다고 하자
$$f(x) = \begin{cases} \frac{1}{2}x^{2} & (-1 \le x < 2) \\ (x - 4)^{2} - 2 & (2 \le x < 5) \end{cases}$$
이 함수는 폐구간 $[-1, 5]$ 에서 연속이다. 따라서 폐구간 방법을 이용할 수 있다.
그리고 이 함수는 미분 가능한 두 개구간 $(-1, 2), (2, 5)$ 과
미분가능하지 않은 한 점 $x = 2$ 로 구성되어 있다.
(구간의 양 끝점에서는 사실 미분 가능하다. 이에 관해 이야기 하면 길어지므로 생략한다.)
1. 우선 임계점부터 살펴보자. 임계점은 미분계수가 $0$ 이거나 존재하지 않게 하는 $x$ 값임을 상기하자.
두 개구간에서는 미분 가능하므로 $f'(x) = 0$ 이 되는 모든 $x$ 값들을 살펴보자.
$x = 0, 4 $ 에서 $f'(x) = 0$ 이 되고 이 때의 함숫값은 각각 $f(0) = 0, f(4) = -2$ 임을 알 수 있다.
그리고 미분불능점인 $x = 2$ 에서의 함숫값은 $f(2) = 2$ 이다.
2. 이제 양 끝점을 살펴보자.
$f(-1) = \dfrac{1}{2}, f(5) = -1$ 이다.
1, 2 에서 구한 모든 함숫값을 나열하면 $0, -2, 2, \dfrac{1}{2}, -1$ 이고
이 중 최댓값은 $2$, 최솟값은 $-2$ 이다.

이전글 : 10. 선형근사 (Linear Approximation)
다음글 : 12. 롤의 정리, 평균값 정리 (Rolle's Theorem, Mean Value Theorem)
'수학 > 미분적분학 (Stewart Calculus)' 카테고리의 다른 글
| 13. 도함수 판정법 (0) | 2022.01.04 |
|---|---|
| 12. 롤의 정리, 평균값 정리 (Rolle's Theorem, Mean Value Theorem) (0) | 2021.02.18 |
| [연습문제] 도함수, 연쇄법칙, 음함수 미분, 선형근사 (5~10) (3) | 2021.01.23 |
| 10. 선형근사 (Linear Approximation) (2) | 2021.01.22 |
| 9. 음함수의 미분법 (Implicit Differentiation) (0) | 2021.01.21 |