다음은 KMO 중학 2023년 기출이다.

풀이 전략은 가우스 기호가 포함된 항과 그렇지 않은 항을 분리시킨 후
그래프를 따로 그려서 교점을 찾는 것이다.
그러려면 가우스 기호가 포함된 함수의 그래프를 그릴 줄 알아야 한다.
우선 주어진 식을 변형하면 다음과 같다.
$$ [x]([x] - 2) = 2x - 4 $$
좌변의 그래프를 그리는 방법을 찾자.
간단히 떠오르는 방법으로는
전체 구간을 양 끝점이 정수인 크기가 $1$ 인 구간으로 쪼갠 후
각 구간에 대해 함수값을 직접 구해서 그래프를 그리는 것이다.
$-2 \le x < -1 \textcolor{orange}{\Longrightarrow} [x]([x] - 2) = -2(-2 - 2) = \textcolor{red}{8} $
$-1 \le x < 0 \textcolor{orange}{\Longrightarrow} [x]([x] - 2) = -1(-1 - 2) = \textcolor{red}{3} $
$0 \le x < 1 \textcolor{orange}{\Longrightarrow} [x]([x] - 2) = 0(0 - 2) = \textcolor{red}{0} $
$1 \le x < 2 \textcolor{orange}{\Longrightarrow} [x]([x] - 2) = 1(1 - 2) = \textcolor{red}{-1} $
$2 \le x < 3 \textcolor{orange}{\Longrightarrow} [x]([x] - 2) = 2(2 - 2) = \textcolor{red}{0} $
$\cdots$
이렇게 해도 되지만 좀 더 쉽게 구하는 방법이 있다.
다음과 같은 아이디어가 있다.
"$[x]([x] - 2)$ 가 사실은 $f(x) = x(x - 2)$ 에 $x = [x]$ 를 대입한 것이다."
이렇게 생각한다면 $f(x) = x(x-2)$ 그래프를 먼저 그린 후에
$x$ 값이 정수인 지점에서의 함수값을 오른쪽으로 다음 정수 $x$ 까지 쭉 이어주기만 하면 된다는걸 알 수 있다.
왜냐하면 함수의 성질에 의해 하나의 $x$ 값에 대해서 오직 하나의 $y$ 값을 주기 때문이다.
무슨 말이냐면 예를 들어 $f(2) = 2(2-2) = 0$ 인데, 인자로 $x$ 대신 $[x]$ 를 넣는다 치면
$2$ 부터 $3$ 미만의 숫자까지는 아무리 대입해도 $2$ 로 바뀌어서 대입이 되기 때문에 모두 그냥 $f(2)$ 랑 같게 된다.
그래서 $2$ 일 때든, $2.1$ 일 때든 $2. 8$ 일 때든 상관없이 $3$ 이 대입되기 전까지
함수값이 $f(2)$ 로써 일정하게 쭉 이어지게되는 것이다.
이 방법대로 직접 그려보면 다음 그림과 같다.
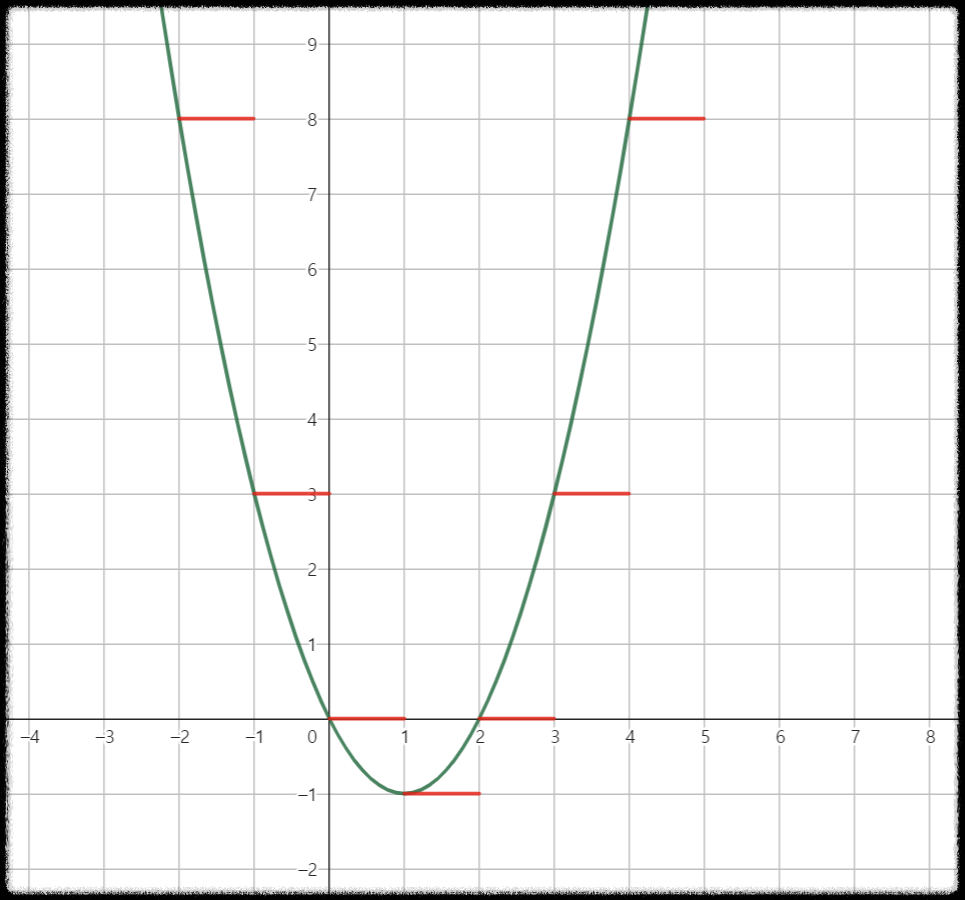
빨간 선으로 표현한 그래프가 $[x]([x] - 2)$ 이고
초록 선으로 표현한 그래프가 $x(x - 2)$ 이다.
이제 $y = 2x - 4$ 를 그려주면 교점을 찾을 수 있다.

$x = 1.5, \; 2, \; 3.5$ 에서 교점을 가지므로 이 $x$ 값을 다 더하면 $S = 7$
참고로 더 이상 교점이 없다는 것은 $3.5$ 이후로 2차함수의 증가가
1차함수보다 가파르다는 것을 이용하면 쉽게 알 수 있다.
그리고 문제에서 $2S$ 를 구하라 했으므로 답은 $14$ 이다.
'수학 > 토막 지식' 카테고리의 다른 글
| $\text{div}$ 가 발산을 나타내는 연산자인 이유 (1) | 2023.10.13 |
|---|---|
| $\text{curl}$ 이 회전을 나타내는 연산자인 이유 (0) | 2023.10.12 |
| 하루에 시계의 시침과 분침은 몇 번 만날까? (0) | 2023.07.28 |
| PDE - Solving heat equation using combination of variables method (0) | 2022.12.09 |
| $f(x+\textcolor{orange}{h})$ 의 테일러 전개가 $ f(x) + f'(x) \textcolor{orange}{h} + \frac{f''(x)}{2}\textcolor{orange}{h^2} + ... $ 인 이유 (1) | 2022.11.26 |