
지난 글에서 일계 미분방정식의 하위 분류 중 선형 일계미분방정식의 경우에는
양변에 적분인자를 곱해준 후 양변을 독립변수에 대해 적분해주면 해를 구할 수 있다는 것을 알았다.
이번에는 일계미분방정식 중 선형이 아님에도 불구하고 특수한 조건 하에는
양변에 적분을 해줌으로써 해를 구할 수 있다는 것을 보일 것이다.
일반적인(General) 일계 미분방정식은 다음 꼴을 갖는다.
$$ \dfrac{dy}{dx} = f(x, y) \tag{식 1}$$
참고로 이번 글에서는 독립변수로 $t$ 대신 $x$ 를 이용할 것이다.
$(\text{식} 1)$ 을 적당히 변형하면 다음과 같은 꼴을 얻을 수 있다.
$$ M(x, y) + N(x, y)\dfrac{dy}{dx} = 0 $$
이렇게 변형하는것은 항상 가능하다.
한 가지 방법으로 $(\text{식} 1)$ 에서 $M(x, y) = -f(x, y)$ 라 하고 $N(x, y) = 1$ 이라고 하면 된다.
이것 말고도 다른 여러 방법이 있을 수 있다. 따라서 이 식 역시 일반적인 일계 미분방정식이다.
이 중 특수한 경우를 선택하자.
만약 $M$ 가 오직 $x$ 만의 함수이고 $N$ 이 $y$ 만의 함수이면 다음과 같다.
$$ M(x) + N(y)\dfrac{dy}{dx} = 0 $$
이 경우, 적분을 통해 바로 해를 찾을 수 있다. 미분형식으로 표현하면 다음과 같기 때문이다.
$$ M(x)dx + N(y)dy = 0 $$
이런 형태의 미분방정식을 변수분리형 미분방정식이라고 부른다.
예제 1
다음 미분방정식을 푸시오.
$$ \dfrac{dy}{dx} = \dfrac{x^2}{1 - y^2} $$
먼저 푸는 방법을 보인 후 이러한 방법이 왜 가능한것인지 설명할 것이다.
우선 이 미분방정식은 변수분리형 미분방정식이다.
왜냐하면 다음과 같이 $M(x) + N(y) \dfrac{dy}{dx} = 0$ 꼴로 변형이 되기 때문이다.
$$ -x^2 + (1 - y^2)\dfrac{dy}{dx} $$
식을 변형하여 다음과 같이 만들자.
$$ (1 - y^2) dy = x^2 dx $$
양변을 부정적분한다.
$$ y - \dfrac{1}{3}y^3 = \dfrac{1}{3} x^3 + C_1 $$
양변에 $3$ 을 곱한 후 식을 정리하여 다음 결과를 얻는다.
$$ x^3 - 3y + y^3 = C $$
따라서 위 등식이 성립하게하는 모든 미분가능한 함수
$y = \phi(x)$ 가 이 미분방정식의 해이다.
이 문제를 푸는 과정에서 다음과 같은 과정을 거쳤다.
$$ \begin{align} &f(x) dx = g(y) dy \\ \Longrightarrow \int &f(x) dx = \int g(y) dy \end{align} $$
왜 양변을 적분해도 되는 것인지 이유를 알아보자면 다음과 같다.
일반적인 변수분리형 미분방정식의 꼴은 다음과 같다고 했었다.
$$ M(x) + N(y)\dfrac{dy}{dx} = 0 \tag{식 1}$$
이 때 $A'(x) = M(x), \; B'(y) = N(y)$ 라고 하면 다음과 같다.
$$ A'(x) + \textcolor{skyblue}{B'(y) \dfrac{dy}{dx}} = 0 \tag{식 2}$$
한편, $y$ 가 $x$ 에 대해 미분가능한 함수라면, 연쇄법칙에 의해 다음이 성립한다.
$$ \dfrac{d}{dx}B(y) = B'(y)y' = \textcolor{skyblue}{B'(y)\dfrac{dy}{dx}} $$
이 결과를 $(\text{식 2})$ 에 반영하면
$$ \dfrac{d}{dx} \bigg[ A(x) + B(y) \bigg] = 0 $$
이제 미적분학의 기본정리에 의해 양변을 $x$ 에 대해 적분하면 다음의 해를 얻는다.
$$ A(x) + B(y) = C \tag{식 3}$$
이는 $(\text{식 1})$ 을 미분형식(Differential form)으로 표현한 다음 식의 양변을 적분한 결과와 같다.
$$ M(x)dx = -N(y)dy $$
따라서 변수분리형 미분방정식의 경우엔 각각의 변수에 대해 미분형식으로 표현한 후
양변을 각각의 변수에 대해 적분하여 푼 것과 결론이 같다.
만약 초기값으로 $y(x_0) = y_0$ 이 주어져 있다면
위에서 얻은 $(\text{식 3})$ 에 이 값을 대입하여 $C$ 를 결정해주기만 하면 된다.
예제 2
다음 초기값을 갖는 미분방정식을 풀고 해가 어떤 구간에서 존재하는지 찾아라.
$$ \dfrac{dy}{dx} = \dfrac{3x^2 + 4x + 2}{2(y - 1)}, \quad y(0) = -1 $$
다음과 같이 식을 변형하자.
$$ 2(y - 1) dy = (3x^2 + 4x + 2) dx $$
변수분리형 미분방정식이므로 양변을 부정적분하여 풀자.
좌변을 $y$ 에 대해 부정적분하고 우변을 $x$ 에 대해 부정적분하면 다음과 같다.
$$ y^2 - 2y = x^3 + 2x^2 + 2x + C, \; \text{C 는 적분상수}$$
초기조건을 만족하는 $C$ 를 찾기 위해 초기값 $y(0) = -1$ 을 대입하여 $C = 3$ 을 얻는다.
따라서 초기값을 만족하는 미분방정식의 음함수꼴 해는 다음과 같다.
$$ y^2 - 2y = x^3 + 2x^2 + 2x + 3 $$
이 해의 좌변에 $1$ 을 더해 완전제곱꼴로 만들 수 있으므로
해를 양함수 꼴로 만들어주면 다음을 얻는다.
$$ y = 1 \pm \sqrt{x^3 + 2x^2 + 2x + 4} $$
플러스 마이너스의 두 가지 해 중 초기조건 $y(0) = -1$ 을 만족하는 해는 마이너스일 때이다.
따라서 초기조건을 만족하는 양함수 해는 다음과 같다.
$$ y = \phi(x) = 1 - \sqrt{x^3 + 2x^2 + 2x + 4} $$
이 함수가 유효한 $x$ 범위를 찾기 위해서는 루트안의 값이 양수가 되는 $x$ 를 찾아야 한다.
루트안의 식 $x^3 + 2x^2 + 2x + 4$ 는 $(x+2)(x^2 + 2)$ 로 인수분해되고 최고차항 계수가 양수이므로
$x > -2$ 에서 양의 값을 갖는다.
따라서 $x > -2$ 의 구간에 해가 존재한다.
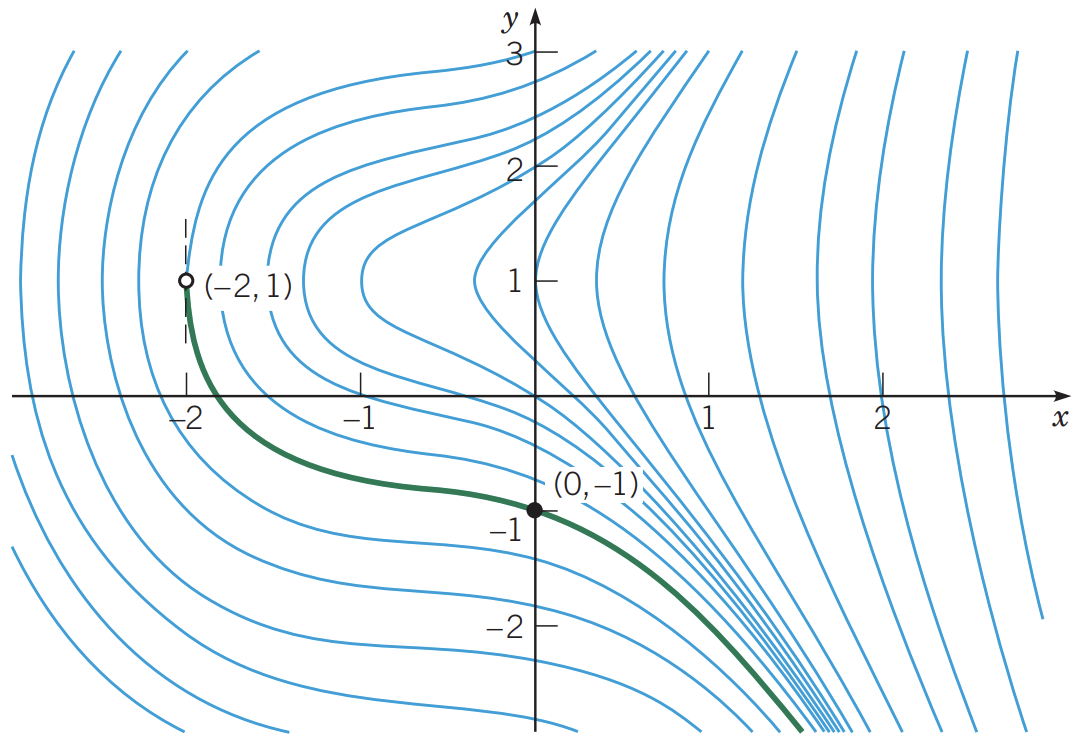
위 그림의 곡선은 이 미분방정식이 가질 수 있는 방향장(Direction Field)을 이은것으로
초록색으로 표현된 곡선이 주어진 초기값의 해를 나타낸다.
해가 유효한 구간이 곡선이 수직이 되는 점 $( x = -2)$ 에서 결정이 된다는 사실을 주목하자.
'수학 > 미분방정식 (Differential Equation)' 카테고리의 다른 글
| 5. 완전 미분방정식 (Exact Differential Equation) (0) | 2022.07.10 |
|---|---|
| 4. 선형/비선형 미분방정식 해의 존재성과 유일성 (2) | 2022.03.01 |
| 2. 적분인자를 이용한 선형미분방정식 해법 (0) | 2022.01.19 |
| 1. 미분방정식의 분류 (0) | 2022.01.04 |
| 미분방정식 들어가기 앞서 (0) | 2022.01.04 |