
가장 먼저 상미분방정식 (미분과 연관된 함수가 일변수함수) 에 대해 다룬다.
다음과 같은 미분방정식이 상미분방정식이다.
$$ \dfrac{dy}{dt} = f(t, y) $$
여기서 $f(t, y)$ 는 독립변수 $t$ 와 $t$ 에 대한 종속변수 $y$ 에 관한 이변수함수로써 그 형태가 정해진것이 없다.
그리고 임의의 형태의 $f$ 가 주어졌을 때 항상 해를 이끌어내는 일반적인(General)한 방법은 아직 알려진게 없다.
하지만 $f$ 가 특수한 조건을 만족하는 경우에 대해서는 일반적인 해법이 존재하는 경우가 있다.
이번 글에서는 $f$ 의 변수 $y$ 가 선형적일 때 미분방정식을 푸는 법을 알아볼 것이다.
미분방정식의 분류가 기억이 안난다면 이 글을 읽어보고 오면 된다.
다음과 같은 형태를 만족하는 미분방정식은 1계 선형 상미분방정식(1st order linear ODE)이다.
$$ \dfrac{dy}{dt} + p(t)y = g(t) \tag{식 1}$$
왜 $g(t)$ 만 등호 오른쪽으로 넘겨서 표현했는지 의문이 들 수도 있는데,
이렇게 정리해 두는게 이후에 나올 개념 설명하는데 편리하기 때문에 $g(t)$ 항과 나머지를 분리했다.
참고로 이후에 나올 내용으로, $ g(t) = 0 $ 이면 이 미분방정식은 동차(Homogeneous)라고 한다.
위의 미분방정식을 다음과 같이 표현할 수도 있다.
$$ P(t)\dfrac{dy}{dt} + Q(t)y = G(t) \tag{식 2}$$
물론 $P(t) \neq 0$ 이라면 양변에 $P(t)$ 로 나누어서 $(\text{식} 1)$ 으로 변형할 수 있다.
$(\text{식} 2)$ 은 때때로 양변을 $t$ 에 대해 적분하여 해를 바로 구할 수 있다.
다음 예제를 보자.
예제1
다음 미분방정식의 해를 구하시오.
$$(4 + t^2)\dfrac{dy}{dt} + 2ty = 4t$$
좌변을 보고 $(4 + t^2)y$ 를 $t$ 에 대해 미분한것임을 눈치채자.
연쇄법칙에 의해 다음이 성립한다.
$$\dfrac{d}{dt} \left[ (4 + t^2)y \right] = (4 + t^2)\dfrac{dy}{dt} + 2ty$$
따라서 식은 다음과 같다.
$$ \dfrac{d}{dt} \left[ (4 + t^2)y \right] = 4t$$
미적분학의 기본정리에 의해 양변을 $t$ 에 대해 적분하면 다음과 같다.
$$ (4 + t^2)y = 2t^2 + C, \quad \text{C is a constant} $$
$(4 + t^2) \neq 0$ 이므로 양변에 이것으로 나누어주어 다음 결과를 얻는다.
$$ y = \dfrac{2t^2}{4 + t^2} + \dfrac{C}{4 + t^2} $$
위의 예제에서는 양변을 $t$ 에 대해 적분하여 바로 해를 구할 수 있었다.
대부분의 선형미분방정식은 위의 예제처럼 바로 적분이 가능하지는 않다.
하지만 라이프니츠는 선형미분방정식의 양변에 어떠한 식 $\mu (t)$ 를 곱하면
위의 예제처럼 양변을 적분하여 바로 해를 구할 수 있다는 것을 알아냈다.
이 때의 $\mu (t)$ 를 적분인자(integrating factor) 라고 부른다.
이제 문제는 적분인자를 어떻게 구하냐는 것이다.
결론부터 말하자면 미분방정식 $y' + p(t)y = g(t)$ 의 적분인자는 $\mu(t) = e^{\int p(t) \; dt}$ 이다.
우선 가장 일반적인 선형미분방정식으로 돌아오자.
$$ \dfrac{dy}{dt} + p(t)y = g(t) $$
양변에 미지의 적분인자 $\mu (t)$ 를 곱하면 다음과 같다.
$$ \textcolor{orange}{ \bigg[ } \mu(t)\dfrac{dy}{dt} + \textcolor{skyblue}{\mu(t)p(t)}y \textcolor{orange}{ \bigg] } = \mu(t)g(t) \tag{식 3}$$
이 때, 이 식의 좌변이 $\mu(t) y$ 를 미분한 결과라고 가정하자.
왜냐하면 우리는 양변을 $t$ 에 대해 적분하여 해를 구하고 싶기 때문이다.
한편 $\dfrac{d}{dt}[\mu(t)y] = \textcolor{orange}{ \bigg[ } \mu(t)\dfrac{dy}{dt} + \textcolor{skyblue}{\dfrac{d\mu(t)}{dt}}y \textcolor{orange}{ \bigg] } $ 이므로 $ \textcolor{skyblue}{\dfrac{d\mu(t)}{dt}} = \textcolor{skyblue}{\mu(t)p(t)}$ 가 성립 해야한다.
즉, 잠시 $\mu(t) > 0$ 이라고 가정하면 다음을 얻고
$$\dfrac{1}{\mu(t)} \dfrac{d\mu(t)}{dt} = p(t)$$
그리고 양변을 $t$ 에 대해 적분하면
$$ \ln{|\mu(t)|} = \int p(t) \; dt + K $$
이 때 $K = 0$ 을 택하자. 그러면 $\mu(t)$ 는 다음과 같다.
$$ \mu(t) = e^{\int p(t) \; dt} $$
이렇게 구한 $\mu(t)$ 를 $y' + p(t)y = g(t)$ 의 양변에 곱해주어
$\mu(t) y' + p(t) \mu(t) y = \mu(t)g(t)$ 로 만들어주면 이 식은 $\dfrac{d}{dt} [\mu(t) y] = \mu(t)g(t)$ 랑 같다.
그리고 이 것은 미적분학의 기본정리에 의해 양변을 $t$ 에 대해 적분하여 간단하게 해를 구할 수 있는 꼴이다.
즉, 해가 존재하는 범위 내의 $t$ 값 중 임의의 $t = t_0$ 에 대해
$$ \mu(t) y = \int_{t_0}^{t} \mu(s) g(s) ds + C $$
이고 양변을 $\mu(t)$ 로 나누어주면 다음과 같이 일반 해를 구할 수 있다.
$$ y = \dfrac{1}{\mu(t)} \left[ \int_{t_0}^{t} \mu(s)g(s) ds + C \right] $$
(단 $\mu(t) = 0$ 이 아닌 구간을 택해야 한다.)
예제 2
다음 초기값을 갖는 미분방정식의 해를 구하시오
$$ \begin{align} ty' + 2y &= 4t^2 \\ y(1) &= 2 \end{align} $$
초기값이 $y(1) = 2$ 라고 주어져 있으므로 $t = 1$
즉 $t = 1$ 근처에 대해서 생각하면 충분하다.
$t > 0$ 라고 가정한 후 양변에 $t$ 로 나누어 변형해주면 다음을 얻는다.
$$ y' + \dfrac{2}{t}y = 4t \tag{식 4}$$
따라서 적분인자는 다음과 같다.
$$\mu(t) = e^{\int \frac{2}{t} \; dt} = e^{2\ln{|t|}} = t^2$$
$(\text{식} 4)$ 양변에 적분인자 $t^2$ 를 곱해주면
$$ t^2 y' + 2ty = 4t^3 $$
한편 좌변은 $\mu(t)y = [t^2y]'$ 이므로 양변을 $t$ 에 대해 적분해주면
$$ t^2 y = t^4 + C $$
$t > 0$ 이므로 양변을 $t^2$ 로 나누어 다음 결과를 얻는다.
$$ y = t^2 + \dfrac{C}{t^2} $$
$y(1) = 2$ 이므로 $t = 1$, $y = 2$ 를 대입하면 $C = 1$ 을 얻고
이 미분방정식의 해를 다음과 같이 얻는다.
$$ y = t^2 + \dfrac{1}{t^2}, \quad t>0 $$
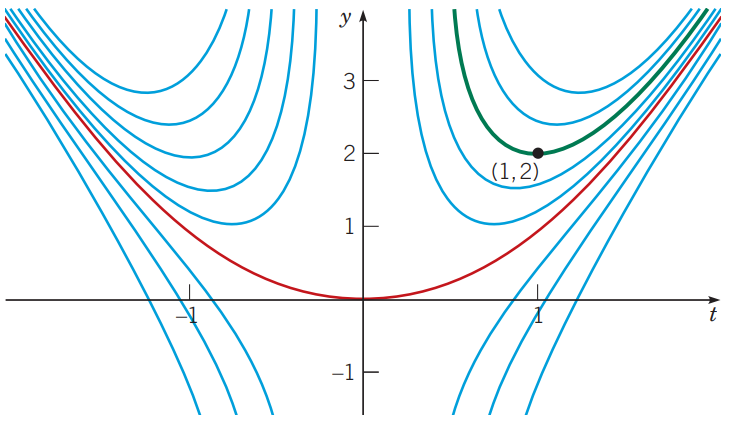
때때로 문제를 푸는 과정에서 적분식이 초등함수로 표현이 안될 때가 있다.
이럴 때는 그냥 적분 상태로 두면 된다.
다음 초기값 문제가 그 예시이다.
$$ \begin{align} 2y' + ty &= 2 \\ y(0) &= 1 \end{align} $$
풀이는 생략한다. 해는 다음과 같다.
$$ y = e^{-\frac{t^2}{4}} \int_{0}^{t} e^{ \frac{s^2}{4} } \; ds + e^{-\frac{t^2}{4} }$$
'수학 > 미분방정식 (Differential Equation)' 카테고리의 다른 글
| 5. 완전 미분방정식 (Exact Differential Equation) (0) | 2022.07.10 |
|---|---|
| 4. 선형/비선형 미분방정식 해의 존재성과 유일성 (2) | 2022.03.01 |
| 3. 변수 분리형 미분방정식과 해법 (0) | 2022.01.20 |
| 1. 미분방정식의 분류 (0) | 2022.01.04 |
| 미분방정식 들어가기 앞서 (0) | 2022.01.04 |