
지금까지 선형 미분방정식의 적분인자를 이용한 해법과 변수분리형 미분방정식의 풀이법을 알아보았다.
여기서 두 가지 의문이 남는다.
구한 해는 과연 그것 뿐일까? 만약 유일하지 않다면 미분방정식을 푸는 의미가 별로 없을 것이다.
또 미분방정식을 풀어보지 않고 해가 존재하는지 바로 알 수 있을까?
이번 글에서는 미분방정식이 특정한 조건 하에서는 해가 항상 유일하게 존재한다는 것에 대해 다룰 것이다.
우선 선형인 경우에 대해 알아보자.
■ 일계 선형미분방정식의 해의 존재성과 유일성에 대한 정리
만약 함수 $p$ 와 $g$ 가 $t = t_0$ 을 포함하는 구간 $I : \alpha < t < \beta$ 에서 연속이라면
다음의 미분방정식
$$ y' + p(t)y = g(t) $$는 구간 $I$ 에서 위의 미분방정식을 만족하는 유일한 해 함수 $y = \phi(t)$ 가 존재하고
초기조건
$$ y(t_0) = y_0 $$을 만족한다.
이 정리는 일계 선형미분방정식은 해가 존재하고 게다가 유일하다는 말을 하고 있다.
그리고 해는 초기값 $t_0$ 이 속하는 구간 $I$, 즉 $p$ 와 $g$ 가 연속인 점에서 존재한다는 말을 하고 있다.
다른 말로, $p$ 나 $g$ 가 불연속이 되는 점에서만 해가 존재하지 않거나 불연속이 된다는 것이다.
이 정리의 증명은 이 글의 일반적인 선형미분방정식 적분인자 구하는 법 유도 과정에서 시작된다.
위의 과정 중에서 적분인자는 다음과 같이 지수함수와 적분식의 합성함수이다.
$$ \mu(t) = e^{\int p(t) dt} $$
$p(t)$ 가 구간 $I$ 에서 연속이므로 미적분학의 기본정리에 의해 $\int p(t) dt$ 는 구간 $I$ 에서 잘 정의되고 미분가능하다.
또 $e^t > 0$ 이고 실수 전체에서 미분가능하며 연속이므로
$e^t$ 와 $\int p(t) dt$ 의 합성함수인 $\mu(t)$ 는 구간 $I$ 에서 미분가능하다. (따라서 연속이다.)
이제 유도과정 중 거의 마지막 부분에 있는 다음 식을 보자.
$$ \dfrac{d}{dt}[\mu(t)y] = \mu(t) g(t) $$
주어진 조건에 의해 $g(t)$ 역시 구간 $I$ 에서 연속이므로 $\mu(t) g(t)$ 는 구간에서 연속이고 따라서 적분 가능하다.
이렇게 적분인자를 이용한 해법이 가능한 풀이라는 것을 보였다.
마지막으로 초기값 $y(t_0) = y_0$ 을 대입하여 적분상수 $C$ 를 결정할 수 있고
이것으로 해가 유일하게 존재하게 되므로 증명이 완료된다.
이번엔 비선형 일계 미분방정식에 대한 해의 존재성과 유일성에 대한 정리를 살펴보자.
■ 비선형 일계 미분방정식의 해의 존재성과 유일성에 대한 정리
함수 $f$ 와 $\dfrac{\partial f}{\partial y}$ 가 점 $(t_0, y_0)$ 을 포함하는 사각 영역 $\alpha < t < \beta, \quad \gamma < y < \delta$ 에서 연속이면
$\alpha < t < \beta$ 속에 포함된 어떤 영역 $t_0 - h < t < t_0 + h$ 에서
다음과 같은 초기값을 가진 미분방정식을 만족하는 유일한 해 $y = \phi(t)$ 가 존재한다.
$$ y' = f(t, y), \quad y(t_0) = y_0 $$
이 정리에 대한 증명은 어렵기 때문에 소개하지 않는다고 되어있다.
정리를 살펴보자.
$y' = f(t, y)$ 에서 우변은 그냥 $t$ 와 $y$ 로 구성된 임의의 식이라고 생각하면 된다.
즉 처음 소개한 정리와 달리 선형이 아니더라도 임의의 일계 미분방정식에 적용할 수 있는 정리이다.
그리고 선형일때의 정리와는 달리 $t_0 - h < t < t_0 + h$ 안에 존재한다는 조건이 붙었는데,
단순히 해의 존재성만 보이고자 한다면 이 조건은 필요없다.
사실 오직 해의 존재성만 보이고자 한다면 $\dfrac{\partial f}{\partial y}$ 조건도 필요없고
$f$ 가 연속이기만 하면 해는 존재한다고 한다. (유일성은 보장 못하지만)
두 번째 정리에서, $f$ 가 연속이면 해가 존재한다는 것을 얘기한다고 했지만,
해가 오직 $f$ 가 연속일때'만' 존재 한다는 것은 아니다.
어떠한 명제 $p \to q$ 가 참일 때, $p \leftrightarrow q$ 역시 참인 것은 아니라는 점에 유의해야 한다.
다음 식을 보자.
$$ \dfrac{dy}{dx} = \dfrac{3x^2 + 4x + 2}{2(y - 1)}, \quad y(0) = -1 $$
비선형 일계 미분방정식의 해의 존재성과 유일성 정리를 적용해보면,
$f(x, y) = \dfrac{3x^2 + 4x + 2}{2(y-1)}, \quad \dfrac{\partial f}{\partial y}(x,y) = - \dfrac{3x^2 + 4x + 2}{2(y-1)^2}$ 이므로
이 둘은 각각 직선 $y = 1$ 을 제외한 모든 영역에서 연속이다.
따라서 정리에 의해 $(t_0, y_0) = (0, -1)$ 을 포함하는 어떠한 사각 영역이 존재하여,
이 영역 내에서 이 미분방정식의 유일한 해가 존재한다.
그런데 초기 조건을 $y(0) = 1$ 로 바꿔도 해가 여전히 존재할까?
이렇게 되면 위에서 말한 존재성/유일성 정리에는 위배된다.
왜냐하면 $y = 1$ 직선 외의 영역에서 $f$ 와 $\dfrac{\partial f}{\partial y}$ 가 연속이라고 했는데
초기 조건으로 $y = 1$ 인 점이 들어가버렸기 때문이다.
하지만 이 미분방정식은 변수분리형 미분방정식이고 이 글에서 보였듯
$x, \; y$ 항을 분리시킨 후 적분하여 해를 얻어낼 수 있다.
변수를 분리한 후 적분하여 $y^2 - 2y = x^3 + 2x^2 + 2x + C$ 를 얻고
초기조건 $x = 0$ 과 $y = 1$ 을 대입하여 $C$ 를 구한다. 정리하면 다음과 같다.
$$ y = 1 \pm \sqrt{x^3 + 2x^2 + 2x} $$
루트 안이 양수여야 하므로 $x > 0$ 에서 해가 존재한다.
앞에서 존재성/유일성 정리 조건을 만족하지 않아도 해가 존재할 수 있다고 한 예시가 바로 이 문제이다.
추가로, $\pm$ 으로 묶여있지만 이는 해가 두 개라는 것에 주의하자.
이 역시 존재성/유일성 정리 조건에 위반될 때는 해가 유일하지 않을 수 있다는 바를 재확인 시켜준다고 볼 수 있겠다.
한편, 비선형 미분방정식의 해의 존재성과 유일성 정리를 만족하지 않더라도 해가 존재하는 또다른 예시가 있다.
$$ y' = y^{\frac{1}{3}} , \quad y(0) = 0 $$
이 미분방정식의 $f(t, y)$ 는 $ y^{\frac{1}{3}} $ 이므로,
$\dfrac{\partial f}{\partial y} = \dfrac{1}{3} y^{-\frac{2}{3}}$ 이라서 $ t = 0 $ 에서 연속이 아니라서 위 정리의 조건을 만족하지 않는다.(분모가 0이 되므로)
하지만 앞서 $f$ 가 연속이기만 하면 유일성은 보장 못해도 해는 존재는 한다고 했었다.
($\dfrac{\partial f}{\partial y}$ 말고 $f$ 얘기니 헷갈리지 않게 주의. $f = y^{\frac{1}{3}}$ 은 실수전체에서 연속이다.)
가장 쉽게 알 수 있는 해는 $y = 0$ 이다. 직접 대입해보면 맞다는 것을 알 수 있다.
이번에는 변수분리형 미분방정식으로 보고 해를 구해보자.
$ y^{\frac{1}{3}} dy = dt $ 이므로 양변을 적분하면 $ \dfrac{3}{2} y^{\frac{2}{3}} = t + C $ 이고 초기값을 만족하는 $C = 0$ 이다.
따라서 $ y^2 = \left[ \dfrac{2}{3}t \right]^3 $ 이고 $y = \pm \left[ \dfrac{2}{3}t \right]^{\frac{3}{2}}, \quad (t \ge 0)$ 이다.
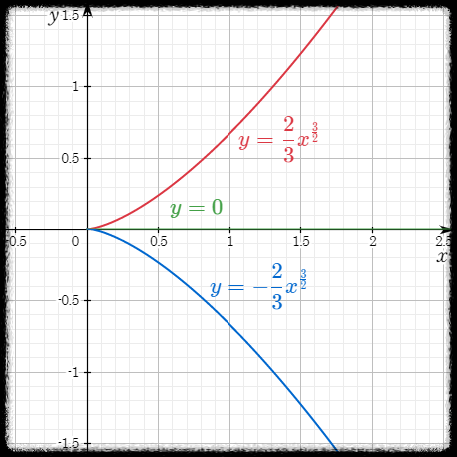
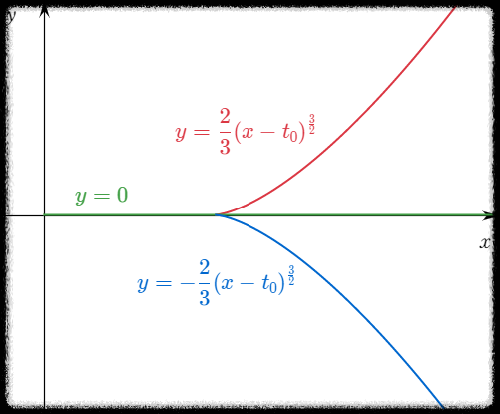
만약 초기값이 $y(0) = 0$ 이 아니라 임의의 초기값 $t_0$ 에 대해 $y(t_0) = 0$ 이였다면,
위에서 구한 방법을 따라가서 다음과 같은 해를 얻는다.
$$ y = \begin{cases} 0, \quad & (0 \le t < t_0) \\ \pm \left[ \dfrac{2}{3}(t-t_0) \right]^{\frac{3}{2}}, \quad & (t_0 \le t) \end{cases} $$
이번에는 해가 존재하는 구간에 대해 알아볼 것이다. 다음 선형 일계 미분방정식을 보자.
$$ y' + p(t) y = g(t), \quad y(t_0) = y_0 $$
이 미분방정식은 처음 소개했던 일계 선형미분방정식의 해의 존재성과 유일성 정리에 의해
$p(t), \; g(t)$ 가 연속인 구간들 중 $t_0$ 이 속해있는 구간에서 항상 해가 존재한다.
즉, $p(t), \; g(t)$ 가 연속이 아닌 곳에서 해가 끊길(불연속) 가능성이 존재한다는 말이다.
여기서 주의해야 할 것으로, 해가 불연속일 가능성이 존재한다는 것이지 무조건 불연속이란건 아니다.
$p(t), \; g(t)$ 가 불연속인 점인데도 불구하고 해가 쭉 이어지는 케이스가 존재한다.
$$ ty' + 2y = 4t^2, \quad y(1) = y_0 $$
이 미분방정식을 적분인자 풀이법으로 구하면 다음과 같다.
$$ y = t^2 + \dfrac{y_0 - 1}{t^2}, \quad t>0 $$
여기서 $y_0 \neq 1$ 이면,
가령 $y_0 = 2$ 라면 $y = t^2 + \dfrac{1}{t^2} \; t>0$ 이므로 다음과 같은 그래프가 나온다.
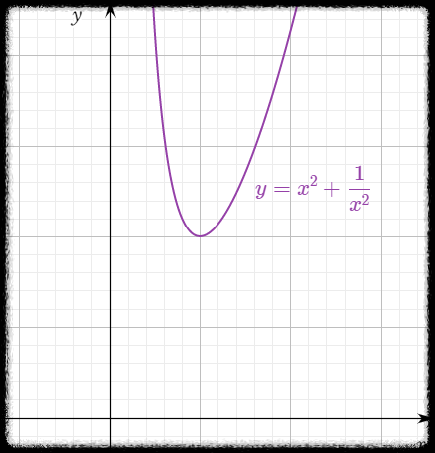
$p(t) = \dfrac{2}{t}$, $g(t) = 4t$ 인데,
위 그림에서 볼 수 있듯이 $p(t)$ 가 불연속이 되는 점 $t=0$ 에서 해도 역시 불연속이다.
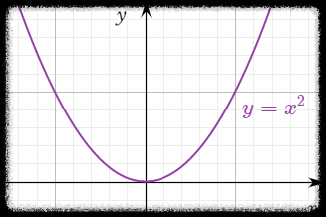
하지만 $y_0 = 1$ 이라면, $y = t^2$ 이 되어서 다음 그림처럼 $t = 0$ 에서도 연속인 해가 나온다.
반면 비선형 일계 미분방정식의 경우에는
존재성과 유일성 정리를 만족한다 하더라도 $h$ 값이 존재한다일 뿐
$h$ 가 그 구간 전체를 덮을 만큼 큰지 아닌지 전혀 알 수 없다.
이해를 돕기 위해서 그림을 그려보자면 이런 느낌이다.

결론적으로 비선형 일계 미분방정식인 경우에는, standard form 만 보고서는 해가 어디서 불연속일지
전혀 예측할 수 없다.
$$ y' = y^2, \quad y(0) = 1 $$
우선 이 미분방정식은 비선형임을 확인하자.
존재성과 유일성 정리에 의하면, $f(t, y) = y^2$ 이고 $\dfrac{\partial y}{\partial t} = 2y$ 이므로 모든 점에서 연속이다.
해를 찾기 위해 변수를 분리하여 적분하자.
$$ \begin{align} \dfrac{1}{y^2} dy &= dt \\ -\dfrac{1}{y} &= t + C \\ y &= -\dfrac{1}{t + C} \end{align} $$
초기값을 만족하려면 $C = -1$ 이어야 하므로 다음과 같다.
$$ y = \dfrac{1}{1-t} $$
명백히 $t \to 1$ 에서 무한으로 발산하므로, 이 $t=1$ 이 해의 불연속이 되게 하는 값이다.
그런데 이는 원래 식 $y' = y^2$ 에서 그 힌트를 전혀 찾아볼 수 없다.
지금까지 살펴보았듯, 일계 선형미분방정식은 비선형 미분방정식인 경우에 비해
알려진 정리로 많은 것을 알아낼 수 있다.
첫 번째로 $p(t), \; g(t)$ 가 연속이기만 하면, 상수를 포함하는 유일한 형태의 해가 존재하고,
초기값이 변함에 따라 가능한 모든 해들은 오직 상수값을 변화시키며 얻어낼 수 있다.
(이런 경우를 앞으로는 General Solution 또는 일반 해 라고 부를 것이다.)
두 번째로, 해가 불연속인 점이 $p(t), \; g(t)$ 가 불연속인 점에서만 존재해서
해의 불연속점을 예측하기 용이하다.
세 번째로, 해를 양함수 형태 $\displaystyle y = \dfrac{1}{\mu(t)}\bigg[ \int_{t_0}^{t} \mu(s)g(s) \; ds + C\bigg]$ 로 얻어낼 수 있다.
미분방정식을 풀어서 음함수꼴이 아닌 양함수꼴로 쉽게 변형이 되도록 해가 구해지는 경우는
그렇게 많지 않다.
반면 일계 비선형 미분방정식은 이 세 가지 모두 참이 아니다.
상수를 포함하는 해를 얻었다 하더라도 그 해가 과연 가능한 모든 해인지 알 수 없다.
거기다 앞서 살펴본 예시처럼 해의 불연속점을 식만 봐서는 전혀 예측 불가능 하고
해를 어찌어찌 구해도 양함수 꼴이 아닌 음함수 꼴로 나오는 경우가 많은 것을
앞으로 문제 풀면서 느낄 수 있을 것이다.
'수학 > 미분방정식 (Differential Equation)' 카테고리의 다른 글
| 6. 수치적 근사법으로 해 구하기-오일러의 방법 (Numerical Approximation-Euler's Method) (0) | 2022.08.04 |
|---|---|
| 5. 완전 미분방정식 (Exact Differential Equation) (0) | 2022.07.10 |
| 3. 변수 분리형 미분방정식과 해법 (0) | 2022.01.20 |
| 2. 적분인자를 이용한 선형미분방정식 해법 (0) | 2022.01.19 |
| 1. 미분방정식의 분류 (0) | 2022.01.04 |